Cyclic Quadrilateral

A four-sided polygon inscribed in a circle is known as a cyclic quadrilateral. With the supplied side lengths, it has the largest possible area. In other words, a quadrilateral encircled in a circle represents the largest possible area for the given side lengths. In this article, we’ll learn more about cyclic quadrilaterals and their properties.

Body

Quadrilateral 

A quadrilateral is a closed figure that has four sides, four vertices, and four angles. It is a kind of polygon with four sides, four vertices, and four angles. There are four non-collinear points that are linked together to form the shape of the letter “A.” The total of all of the internal angles of a quadrilateral is always 360 degrees. 

What is cyclic quadrilateral and its properties?

A cyclic quadrilateral is a quadrilateral that is encircled by a circle of any size. In other words, a circle travels around each of the quadrilateral’s four vertices four times. Concyclic vertices are those that are organised in a circular manner on a graph or in a table. The circumcenter of a circle is called the circumcenter, and the circumradius is called the circumradius.

“Cyclic” is derived from the Greek word “kuklos,” which means “circle” or “wheel.” The term “quadrilateral” comes from the Latin word “quadri,” which means “four sides” or “latus.”

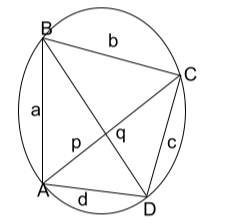
ABCD is a cyclic quadrilateral with side-lengths a, b, c, and d and diagonals p and q, as shown in the diagram below.

Properties

The properties of a cyclic quadrilateral make it easy to recognise this figure and answer problems based on it. The following are some of the properties of a cyclic quadrilateral:

• In a cyclic quadrilateral, all four of its vertices are located on the circumference of the circle that forms the quadrilateral. 
• The four chords of the circle correspond to the four sides of the quadrilateral that has been written. 
• Internal angles are equal to the measure of an external angle at a vertex when they are in opposition. 
• In the case of a cyclic quadrilateral, the total of the products of the opposing sides is equal to the product of the diagonals of p and q. 
• The perpendicular bisectors are always parallel to one another, regardless of their orientation. 
• The perpendicular bisectors of the four sides of the cyclic quadrilateral come together at the point O in the centre. 

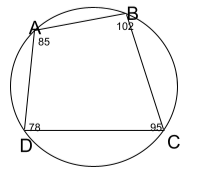
180° is the sum of two opposed angles (supplementary). The four angles of an inscribed quadrilateral are ∠A, ∠B, ∠C, and ∠D. After that, ∠A+∠C=180° and ∠B + ∠D =180°.

Theorems related to cyclic quadrilateral

Ptolemy Theorem

According to Ptolemy’s theorem, in a cyclic quadrilateral with consecutive vertices A, B, C, and D, the sides a = AB, b = BC, c = CD, d = DA, and the diagonals p = AC and q = BD are the same. It is possible to describe diagonals in terms of sides using the formula p * q = (a * c) + (b * d). 

Brahmagupta Theorem

In geometry, Brahmagupta’s formula is used to compute the area of any quadrilateral with specified sides, and it may be found here. The area K of a cyclic quadrilateral with sides of lengths a, b, c, and d, where s is the semi-perimeter, is equal to the sum of the squares of its sides. However, there were various difficulties encountered with this theory, like as 

• What is the best way to demonstrate that a quadrilateral is cyclic? 
• What is a non-cyclic quadrilateral, and how does it work? 

And that’s why it failed.

General theorems that are used to solve questions

Theorem1: In a cyclic quadrilateral, the total of one pair of opposed angles is additional to the other pair of opposite angles. 

This theorem will now be shown, so let’s get started. 

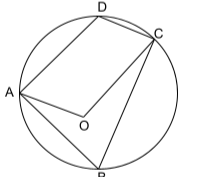
It is shown that the cyclic quadrilateral ABCD is surrounded by a circle with the centre O. 

Connect the vertices A and C to the centre O by drawing a line across them. 

Likewise, the converse of this theorem (which asserts that if opposing angles of a quadrilateral are supplementary, the quadrilateral is cyclic) is true.

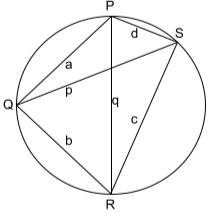
Theorem2: The Cyclic quadrilateral theorem can be used to calculate the ratio between the diagonals and the sides. The product of the diagonals of a quadrilateral inscribed in a circle is equal to the total of the product of its two pairs of opposite sides.

PQ and RS, as well as QR and PS, are opposing sides of a cyclic quadrilateral PQRS. The diagonals are PR and QS.

PR x QS = (PQ x RS) + (QR x PS)

Conclusion

As a result, we can infer that the cyclic quadrilateral has many qualities that are comparable to those of a quadrilateral, and we have gone over several concepts in this regard. In a number of geometry issues, cyclic quadrilaterals are very helpful, especially in situations that involve angle chasing. p * q = sum of the product of opposite sides of a cyclic quadrilateral, where p and q are the diagonals. The perpendicular bisectors are always parallel to each other. At the centre O, the perpendicular bisectors of the four sides of the cyclic quadrilateral meet. 180° is the sum of two opposed angles.