Profile
Settings
Refer your friends
Sign out
The mean value of the product of the deviations of two variables from their respective means is known as Covariance which tells us about the relationship between two variables. We can define it also as a change between the two variables. As a change in one variable is equal to the change in another variable. And this is also the property of a function when it is transformed linearly. In this article, you will study covariance which means, formula, and its relation to correlation.
Covariance
Covariance can be defined as the measure of the variation of two random variables. Using the covariance, you can see the direction of a relationship.
Covariance is of two types:
- Positive Covariance
- Negative Covariance
Positive Covariance
If covariance for any two variables is Positive, which means, that each of the variables in the same direction. Here, the variables show comparable behavior which shows that, if the values (greater or lesser) of one variable correspond to the values of the second variable, then they will be said to be in positive Covariance.
Negative Covariance
If we get the covariance for any two variables is negative, meaning, both the variables move on the contrary path. It is the opposite of positive covariance, wherein greater values of one variable correspond to lesser values of every other variable and vice-versa.
Formula
Covariance Formula, A statistical Formula that is used to assess the relationship between variables. Let us say X and Y are any two variables, whose covariance has to be calculated. The covariance of those variables is denoted by using Cov(X, Y). The following formula is used for finding both population covariance and sample covariance.
Population Covariance
Covariance for two variables X and Y
- If Cov(X, Y) > 0, then the covariance of the two variables is positive that is they are moving in the same direction.
- If Cov(X, Y) < 0, then the covariance of the two variables is negative that is they both are moving in the opposite direction.
- If Cov(X, Y) = 0, then variables are not having any relation between them.
Correlation Coefficient
Correlation estimates the depth of the relationships among variables. We can see it as the estimated measure of covariance and It is dimensionless. In other phrases, the correlation coefficient is a constant value usually and does no longer have any units. It will have a value between one and minus one (-1). When the value is one, variables have a positive correlation. When the correlation coefficient is zero, then there are no relationships between the variables.
The Relation between the correlation coefficient and covariance is given by using;
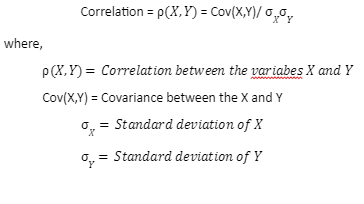
Comparison between Correlation and Covariance
COVARIANCE | CORRELATION |
It’s far a measure to expose the quantity to which given two random variables exchange with respect to every other. | It’s far a measure used to describe how strongly the given random variables are associated with each different. |
It is a degree of correlation. | it is a scaled form of covariance |
The value of covariance lies among -∞ and +∞. | The value of correlation lies between -1 and +1. |
It suggests the direction of the linear dating between the given variables. | It helps us in measuring the direction and strength of the linear relationship among the given variables. |
Example of Covariance
We have provided the example of covariance here, which helps you in understanding much better about covariance.
Ques: Calculate the Covariance Coefficient for the given data.
Relation of Covariance and Correlation
Covariance shows us the different ways as which the variables are different. Whereas, correlation shows us how the given variables are related to each other. The simplest way by which the relationship between covariance and correlation can be related is the same as the relationship between variance and standard deviation.
Conclusion
Covariance tells us about how does mean values of two different variables move together. In Statistics, to understand the relationship between two linear variables, Covariance and correlation both are very useful terms. Further, we have discussed two different types of covariance which are positive covariance and negative covariance. We have given the Covariance formula to carry out the mathematical calculations in statistics. The correlation coefficient has also been discussed. To understand the difference between covariance and correlation we have discussed it in detail. How are covariance and correlation related we have even talked about it.
