Profile
Settings
Refer your friends
Sign out
Introduction
The law of cosines, often known as the cosine rule, is a formula that links the cosine to the three side lengths of a triangle. The rule of cosine aids in determining the link between the lengths of a triangle’s sides and the angles’ cosine. The Pythagoras theorem, which applies to a right triangle, is generalised by the cosine law in trigonometry.
Rule of cosine- statement
The square of any one of a triangle’s sides is equal to the difference between the sums of squares of the other two sides and double the product of the other sides and the cosine angle included between them, according to the rule of cosine.
The cosine rule has two applications:
- If we know the three side lengths of the given triangle, we can apply the cosine rule to get the three unknown angles.
- If we know two side lengths and the angle between them, we can apply the cosine rule to get the third side length of a triangle.
Cosine rule side formula
Consider the ABC oblique triangle below. A non-right triangle is known as an oblique triangle. Keep in mind that the side lengths are written in lowercase letters, while the angles are written in upper case letters.
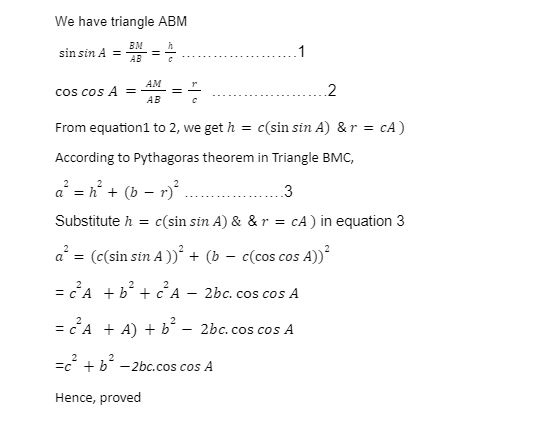
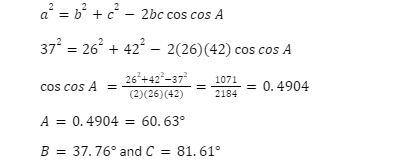
Conclusion
We learn about the cosine rule in this article. In trigonometry, the square of the length of any side of a triangle is equivalent to the total of the squares of the lengths of the other sides minus twice the product of the other two sides multiplied by the cosine of the angle between them. If all three sides of the triangle are known, the cosine rule can be used to calculate any of the angle measures. The cosine rule can also be used to compute the length of the third side if two sides and their angles are known.
