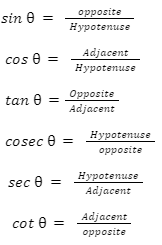Profile
Settings
Refer your friends
Sign out
In mathematics, the meaning of cos is all about the cosine function, which is the concept of trigonometry. The cosine function is one of the important functions which includes the sine function and tangent function also. Hence, the cosine function is a very important function in trigonometry. On the basis of these functions, we can solve the whole trigonometry, by just understanding their few concepts.
We are already aware that the sine function, cosine function, and the tangent function are all applicable to the right- angles triangle. So, talking about the cosine function, let us understand the definition and the concepts related to the cosine function to solve the angle-related mathematical problems.
COS MEANING
In a right-angled, the cosine of an angle is defined as the length of the adjacent side divided by the length of the hypotenuses. In short, cosine is written as cos. It will help you determine the angles of the triangle and even calculate the length of the triangle.
Let us suppose ABC be the right-angled triangle which is right-angled at B. Let α be the angle which is at A. So, in order to calculate the cosine function, also called the cos function, we can say
cos α= AB/AC
COS MEANING FORMULA-
The cos meaning formula is the formula used to calculate the cosine function of the related angle.
In this triangle, we can have
Here, we have the cos angle formula which is used to calculate the angles.
Note-
sin θ= 1/cosec θ
cos θ= 1/sec
tan θ=1/cot
tan θ=sinθ/cosθ
cot θ=cosθ /sinθ
cosec θ=1/sinθ
sec θ=1/cosθ
cos2 MEANING
Trigonometric identities are the identities that are related to different trigonometric functions.
These trigonometric identities are used to relate trigonometric formulas. They are sine, cosine, tangent, cosecant, secant, and tangent.
According to one of the trigonometric identities,
θ+θ=1
Here, θ is an acute angle of the right-angled triangle
Other trigonometric identities are-
θ=1-
cos2θ=2θ-1
Basic Cos Values-
Degree | Value |
0° | 1 |
30° | 32 |
45° | 1√2 |
60° | 12 |
90° | 0 |
Law of Cosine –
The cosine law (cos law) talks about the relationship between the angles and the sides of the triangle. This law is referred to as the law of cosine or cosine rule.
c2=a2+b2-2abcos
Where a, b, and c are the sides of the triangle.
Law of Sine-
The law of sine states that
a/sin A =b/sin B =c/sin C
It is applicable to any triangle. Here, a, b and c are the sides.
A B and C are the angles.
In this, Side a should face angle A, Side b should face angle B, Side c should face angle C.
Sine and tangent function-
Let us, in brief, discuss the sine function and tangent function as well. Above we have talked about the basic formula to use in order to find the angles of the right-angled triangle.
We know that the sine function and tangent function are the primary functions. The sine function is the ratio of the perpendicular side to the hypotenuse. The tangent function is the ratio of perpendicular to the base.
Solved Examples-
Find the trigonometric ratios of tan in terms of cot θ.
Sol- The trigonometric ratios of tan θ in terms of cot θ can be written as
tan θ=1/cot
Find the trigonometric ratios of sec θ in terms of cot θ.
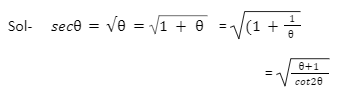
CONCLUSION-
As discussed above we have talked about the importance of the cosine function along with the sine and tangent function in trigonometry. We have seen the definition of the cosine function and why the trigonometric functions are important in mathematics. We have even talked about the cosine formula which can be used in calculating the mathematical operations. We also came across all those functions which are sine function, cosine function, tangent function, cosecant function, secant function, and cotangent function are applicable in a right-angled triangle. We have discussed what is the meaning of meaning.
