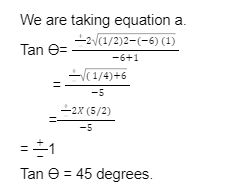Profile
Settings
Refer your friends
Sign out
Lines that are in the same plane are coplanar. These lines are said to be in the same three-dimensional space. Coplanarity of two lines is proved using the condition in vector form and cartesian form.
In a 3-dimensional space-
Two lines are coplanar if there is a plane that includes them both. This is possible only if the lines are parallel or intersect.
Three points are always coplanar, and if they are not collinear, the plane is unique.
Four points may or may not lie in the same plane.
Distance geometry determines whether points are coplanar by determining the distance between them.
Conditions That Determine Coplanarity of Two Lines
Coplanarity is a condition when several lines are located on the same plane.
In 3 dimensional geometry, the Vector form and Cartesian form are used to prove whether two lines are coplanar or not.
Condition of Coplanarity of Two Lines in Vector Form
Equation of line using vector notation is given by:
r → = l1→+ λm1 —————— (1)
r → = l2→ + μm2 ——————– (2)
Here, line (1) passes through a point L with a position vector l1 parallel to m1.
Line (2) passes through a point M having position vector l2 and is parallel to m2.
These two lines are coplanar if and only if
LM→ is perpendicular to m1 x m2
This is given as
LM = l2 – l1
Therefore the condition of coplanarity is given:
LM.(m1 x m2 ) = 0
(l2 – l1). (m1 x m2) = 0
Condition of Coplanarity of Two Lines in Cartesian Form
Condition of coplanarity in Cartesian form emerged from the vector form.
Consider two points
L (a1, b1, c1)
Q (a2, b2, c2) in the Cartesian plane.
Let us assume there are two vectors – q1 and q2.
Their direction ratios are –
x1, y2, z1, and x2, y2, z2.
The vector form of the equation of the line connecting L and Q is given as
LQ = (a2 – a1)i + (b2 – b1)j + (c2 – c1) where Q1 = x1i + y1j + z1 and Q2 = x2i + y2j + z2k
The above condition is used in a vector in order to induce a condition in Cartesian form for calculation purposes.
In the above equation, two lines are said to be coplanar if LQ. (Q1 x Q2) = 0.
Hence, in Cartesian form, the matrix that illustrates this equation is 0.
Another method of explaining through the Cartesian form is explained below-
Let us take two points, A and B. Let the coordinates of A be ( x1,y1,z1 ) and that of B be ( x2,y2,z2 ).
Let us take two vectors, a1 and b1. Let a1,b1,c1 and a2,b2,c2 be the direction vectors.
AB = ( x2-x1 )i + ( y2-y1 )j + (z2-z1 )k
b1=a1i +b1j +c1k and
b2= a2i +b2j +c2k
The above lines are coplanar only if
AB. (b1 X b2 ) = 0.
In the cartesian, form it is expressed as
= 0.
Steps to determine whether the lines are coplanar or not from the 3X3 matrix above-
A 3 X3 matrix is used to store the elements of the determinants.
Calculation of a cross product of b2 and a2 and the dot product of ( a2-a1 ).
On solving the matrix, if the determinant value is 0, then the lines are coplanar.
If the value is not 0, then the lines are not coplanar.
How Can We Prove if Two Vectors Are Planar or Not?
One major coplanarity of two lines questions is how can two vectors be planar or not.
The conditions are as follows:
If the given three vectors are linearly dependent on each other or not.
If the product of 3 vectors is equal to zero.
‘N’ vectors are coplanar if no more than two vectors are independent.
Examples of Coplanarity of Two Lines
Example1:
L1: (x1, y1, z1) = (-3, 1, 5) and (a1, b1, c1) = (-3, 1, 5)
L2: (x2, y2, z2) = (-1, 2, 5) and (a2, b2, c2) = (-1, 2, 5)
=
=0
Lines are Coplanar
Example2:
L1: (x1, y1, z1) = (1, 2, 3) and (a1, b1, c1)= (2, 4, 6)
L2: (x2, y2, z2) = (-1, -2, -3) and (a2, b2, c2) = (3, 4, 5)
=
=0 Lines are Coplanar
Conclusion
Coplanarity of two lines questions in geometry can often confuse us. One practical example of coplanar lines is the lines in exercise copies. The lines are not only coplanar but also parallel to each other. Understanding the coplanarity of two lines notes with emphasis on Vector and Cartesian form is important to determine whether lines are coplane or not. When two lines are not coplanar; they are called skew lines.
