Coordinates of a Point in Space

The Coordinate System

A coordinate system is a system in geometry that employs one or more integers, or coordinates, to define the location of points or other geometric components on a manifold, such as the Euclidean space, in a unique way. The order of the coordinates is important, and they can be recognised by their positions in an ordered tuple or by a letter, as in the x-coordinate.

In elementary mathematics, the coordinates are assumed to be real numbers, but they can be complex numbers or members of a more theoretical system like a commutative ring. Analytic geometry is based on the usage of a coordinate system, which allows problems in geometry to be transformed into problems regarding numbers and vice versa.

The Three dimensional Coordinate System

Two integers are required to locate a point in a plane. 

Any point in the plane can be represented by an ordered pair (a, b) of real numbers, where a represents the x-coordinate and b represents the y-coordinate. As a result, the plane is referred to as two-dimensional. Three numbers are necessary to pinpoint a point in space. Any point in space is represented by a real-number ordered triple (a, b, c).

To represent points in space, we begin with O (the origin) as a fixed point and three perpendicular directed lines passing through O, known as the coordinate axes and designated the x-axis, y-axis, and z-axis. We usually think of the x and y-axes as horizontal and the z-axis as vertical, and we draw the axes in that order.

The right-hand rule determines which way the z-axis will point. Your thumb points in the positive direction of the z-axis if you wrap perform a counterclockwise movement with your right hand’s fingers from the positive x-axis to the positive y-axis of 90 degrees.

The Three-Dimensional Plane

A pair of perpendicular axes define the coordinate plane in two-dimensional space. We can name any position within the plane using these axes. The coordinate axes define coordinate planes in three dimensions, just as they do in two dimensions. There are three intersecting pairs of axes now that there are three axes. The xy-plane, xz-plane, and yz-plane are all coordinate planes made up of two axes. The xy-plane is defined formally as {(x,y,0):x,y}. The xz-plane and the yz-plane, respectively, are defined as {(x,0,z):x,z} and {(0,y,z):y,z}.

Imagine that you are constructing a home and you’re standing in a room with only two of the four walls completed. (Assume the two completed walls are next to one another.) The floor is the xy-plane, the wall to your right is the xz-plane, and the wall to your left is the yz-plane, and  you are standing with your back to the corner where the two finished walls meet, facing out into the room.

The xy-plane is the plane that contains the x and y–axes. The xz-plane is defined by the x and z-axes, while the yz-plane is defined by the y and z-axes.

The plane is divided into four quadrants into two dimensions by the coordinate axes. In the same way, the coordinate planes split space between them into eight octants or regions around the origin. In the same way that quadrants fill two, the octants fill three. There are three non-zero coordinates for points in octants.

Coordinates of a Point

Graphing in xyz-space can be challenging because, unlike graphing in the xy-plane, it requires depth awareness. 

Projection into the coordinate planes can be used to make the plotting of points easier. A point (x, y, z) is projected onto the xy-plane by connecting it to the plane with a line segment that is perpendicular to it and computing the intersection of the line segment with the plane. In this case, our working definition says that the point (x, y, z) projection onto the xy-plane is the point (x, y, 0). Similarly, this point’s projection onto the -plane is point (0, y, z), and its projection onto the xz-plane is point (0, y, z) (x, 0, z). One can plot the point’s projections first, which is comparable to showing points on the xy-plane, and then find the point in xyz-space using line segments originating from these projections and perpendicular to the coordinate planes.

The Distance Formula

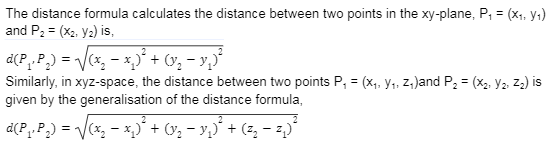
This can be demonstrated by applying the Pythagorean Theorem repeatedly.

Equation of Surfaces

A curve is the solution set of a single equation in two dimensions including the coordinates x and/or y. A surface is the solution set of an equation involving x, y, and/or z in three dimensions.

Examples

The equation z = 3 depicts a plane that is parallel to the xy-plane and 3 units ‘above’ it. That is, it is 3 units apart from the xy-plane along the positive z-axis. The equation x=y, on the other hand, defines a plane in which all points have the same x- and y-coordinates. It is not parallel to any coordinate plane, although it does contain the z-axis, which contains all points with zero x and y coordinates, and it intersects the xy-plane at y=x.

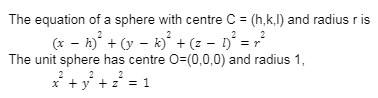
Conclusion

The one-to-one connection between each point P in three-dimensional space, or xyz-space, and an ordered triple (x, y, z) in R3 is called the three-dimensional rectangular coordinate system.

P’s x-, y-, and z-coordinates are denoted by the numbers x, y, and z. The point with coordinates O is called the origin (0, 0, 0). The xy-plane contains all points with a z-coordinate of zero; the yz-plane contains all points with an x-coordinate of zero; and the xz-plane contains all points with a y-coordinate of zero.