A coordinate system is a system through which one can specify the location of points in a plane or 3D (three-dimensional) space. To locate a point in 3D space, three numbers are required, i.e., an ordered triplet of real numbers, on three mutually perpendicular axes. The three axes progress to intersect at a point known as the origin. The three numbers are the coordinate axes that are given, where one is perpendicular to the other two at the origin. This method is a Cartesian geometry method to determine the location of any point in space. There are other methods such as spherical coordinate systems and cylindrical coordinate systems too.
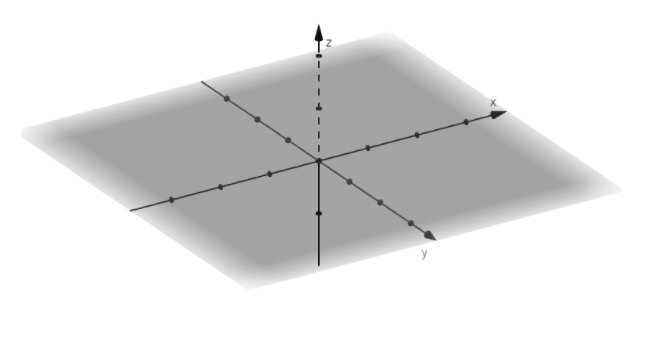
These are the three coordinate axes (in the figure): x-axis, y-axis and z-axis. These three axes are mutually perpendicular to each other. These axes make coordinate planes in space, two axes together make a plane.A coordinate system can also be used to identify the location of vectors in a space.
Coordinate Planes
The three coordinate axes, x-axis, y-axis and z-axis, determine the three coordinate planes. The x and y-axis together make the xy-plane, similarly, the yz-plane consists of the y and z-axis, and the x and z-axis determine the x-plane. The figure given below makes the point clearer.

We can see the three coordinate planes formed by three coordinate axes in the above figure. These three coordinate planes divide the 3D space into 8 parts, known as octants.
The Room Analogy to Explain Coordinate System in 3D Space
Let’s take any corner of your room as the origin. The wall on your left and the floor of the room intersects through a horizontal line, it is the x-axis. The floor of the room and the wall on your right intersect through another horizontal line and that’s the y-axis. Finally, the line through which the wall on your right and left side of the room intersect vertically is the z-axis. Taking into account the above observations, it can be said that the wall to your left is the xz-plane, the floor represents the xy-plane and the right wall is situated in the yz-plane. Now, see the portion of axes present in the room. These are the positive portions of the three coordinate axes and the negative portion of these axes will be available when extended outside the room.
The positive portions of these coordinate axes (x, y, and z-axis) combine to make a right-handed coordinate system. Right-handed coordinate system suggests that if you curl your finger to make a fist of your right hand, your thumb will represent the direction of the z-axis. Now, switching the locations of the positive x and y-axis would make the coordinate system left-handed. Switching the universes leads to a change in some signs in formulas. The right-handed and left-handed coordinate systems show two balanced valid mathematical universes.
Types of Coordinate Systems in 3D Geometry
Cartesian coordinate system
For 3D geometry, the Cartesian coordinate system consists of a triplet to locate any point in space with three mutually perpendicular axes. There are no standard names for the three axes as such, however, the terms ordinate, abscissa, and applicate have been used often. The Cartesian coordinates are non-ambiguous and unique. Therefore, the points are usually written in real numbers. The all ordered triplets of real numbers in the Cartesian coordinate system combine to make a set that is the Cartesian product and is denoted by R3 i.e., R×R×R=(x, y, z), where x, y, z ∈R (real numbers). This one to one relation between the points in space and ordered triplets has been given the name 3-D rectangular coordinate system.
Cylindrical coordinate system
It is a 3D coordinate system that usually helps to determine point positions from a certain reference axis’s distance, the direction from the axis to the certain reference axis, and the distance from a certain reference plane perpendicular to the axis. Cylindrical coordinates are generally used in connection with objects and processes that have some symmetry of rotation about the longitudinal axis.
Spherical coordinate system
It is a 3D coordinate system where the position of a point is specified by three numbers:
Radial distance: It is the distance measured from the origin.
Polar angle: The angle measured from a fixed zenith direction.
Azimuthal angle: The angle of its orthogonal projection on a reference plane passing through the origin and measured from a fixed direction used as a reference on that plane.
The knowledge of polar coordinates helps in learning Spherical coordinates as well.
Cartesian coordinate systems and Spherical coordinate systems are related in some way, and their relationship can be determined using trigonometry.
Conclusion
A coordinate system in 3D geometry is generally used to locate the points in a plane and specify the location of vectors in space. There are three coordinate systems in 3D – Cartesian coordinate system, Spherical coordinate system, Cylindrical coordinate system. In the Cartesian coordinate system, the location of any point is found by a triplet of real numbers, based on the three axes. The set of ordered triplet (R3), locating the point in space also represents a one to one correspondence between any point in space and the ordered triplet itself, known as the rectangular coordinate system. The three axes (x-axis, y-axis and z-axis) form planes when combined individually, two planes join to form one plane. Coordinate geometry is used in some physical situations such as to map geographical locations using latitudes and longitudes, in aviation to determine the position on aerolanes, in digital devices and many more.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






