“The great beauty of a graph is that it is an oblique, difficult to comprehend representation of a wonderful thing made up of lines and knots. Can be reduced.” (Das chinesische Dreieck: die kniffligsten, D. Olivastro. 10000-year-old mathematise Rattle Droemer. Munches: Knauer, 1995, S.273)
Graph transformation, often known as graph rewriting, is a computer science technique for constructing a new graph from an existing one. It has a wide range of applications, from software engineering (software development and verification) to layout algorithms and image production.
Definition
Graph transformations can be used for abstract computations. The core principle is that if a computation’s state can be described as a graph, then subsequent stages can be expressed as transformation rules on that graph. Such rules include an original graph that must be matched to a complete state subgraph and a replacing graph that must replace the matched subgraph.
A graph rewriting system is often composed of a collection of graph rewrite rules of the form display style Lrightarrow R, with display style L referred to as the pattern graph (or left-hand side) and display style R referred to as the replacement graph (or right-hand side of the rule). By searching for an occurrence of the pattern graph (pattern matching, thereby overcoming the subgraph isomorphism problem) and replacing the detected occurrence with an instance of the replacement graph, a graph rewrite rule is applied to the host graph. In the case of labelled graphs, such as string-controlled graph grammars, rewrite rules can be further regulated.
The distinct terminology is designed to stress the objective of constructs, such as the enumeration of all graphs from some starting graph, i.e. the development of a graph language – rather than just translating a given state (host graph) into a new state, as is the case with graph grammar.
Transformation of Y-Coordinate by a Constant
Reflecting a value across the y-axis or another vertical axis is one of the most basic transformations you can perform with simple functions. This could be expressed in a variety of ways in a potential test question, so make sure you recognize the following terms as merely another way of stating “conduct a reflection across the y-axis”:
- Graph y = f(-x)y=f(−x)
- Graph f(-x)f(−x)
- f(-x)f(−x) reflection
- Or simply: f(-x)f(−x)
The procedure for doing so is straightforward: Simply select easy-to-determine coordinates, divide the x-coordinate by (-1), and re-plot those coordinates for any function, no matter how hard it is. That’s everything!
An example problem is the best technique to practice painting reflections over the y axis:
Example
Draw y = f(-x)y=f(x) on the graph of y=f(x)y=f(x) as indicated.
Remember, before charting the f(-x) reflection, all we have to do is divide the x-coordinates of easy-to-determine locations on our graph by (-1). When we say “easy-to-determine points,” we simply mean points for which you know the exact x and y values. Picking points where you must estimate values makes the problem needlessly difficult. The illustrations below will help you visualize how to address this challenge.
Step 1: Recognize that we’re reversing the y-axis.
Step 2: Locate simple-to-determine points.
Step 3: Subtract (-1) from these positions and plot the new points.
Transformation of X-Coordinate by a Constant
The letter “a” also has the effect of reflecting the graph across the x-axis. When the a-value of the parent function f(x) = x² is less than 0, the graph reflects across the x-axis before being converted. The function f(x) = -x² is represented in the graph below.
This reflection is represented as a negative outside the function in function notation: -f (x). There is a reflection across the y-axis if the negative is inside the function notation. Because a parabola is already symmetric about the y-axis, this modification has no effect on its appearance.
A reflection over the x– or y–axis is another transformation that can be given to a function. A horizontal reflection reflects a graph horizontally across the y-axis, while a vertical reflection reflects a graph vertically across the x-axis.
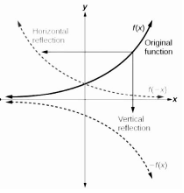
The vertical reflection creates a new graph that is a mirror image of the original or base graph on the x-axis. The horizontal reflection creates a new graph that is a mirror image of the original or base graph on the y-axis.
Construction of y = k c(x) From y = f(x) Where k≠0 Is a Constant
Vertical Translation
The function defined by for the base function f (x) and a constant k is
f (x) + k = g (x),
Shifting f (x) k units vertically can be illustrated.
Horizontal Translation
The function defined by for the base function f (x) and a constant k is
f(x) = g(x) (x – k),
Shifting f (x) k units horizontally can be illustrated.
Vertical Stretches and Shrinks
The function generated by for the basic function f (x) and a constant k > 0 is
g(x) = k f(x)
If k > 1, vertically stretching f (x) by a factor of k can be illustrated. OR
F (x) is vertically shrunk by a factor of k if 0 k 1.
Conclusion
The flow of computing is defined using graphs. Graphs are used to represent communication networks. Data organisation is shown using graphs. Graph transformation systems manipulate graphs in memory using rules. Graph databases store and query graph-structured data in a transaction-safe, permanent manner. The shortest path in a road or a network is determined using graph theory. Various locations are represented as vertices or nodes, while highways are represented as edges, with graph theory being utilised to calculate the shortest path between two nodes in Google Maps.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






