A conic section (or simply conic) is a curve formed by the intersection of the surface of a cone with a plane in mathematics. The hyperbola, parabola, and ellipse are the three forms of conic sections; the circle is a special case of the ellipse, though it was sometimes considered a fourth type. Conic sections are formed when a plane and a cone intersect. Nappes are two equally formed sections of a cone. One nappe is what most people think of when they say “cone,” and it resembles a party hat.
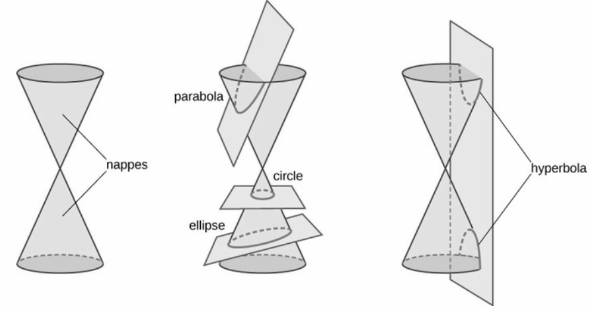
Common Parts of Conic Sections
The focus of the conic section is the point around which it is built. In other words, it is the point at which the curve’s reflected rays converge. An ellipse and hyperbola both have two points of emphasis around which the shape is built.
A directrix is a line that is used to define and create a conic section. The distance between a directrix and a point on a conic section is proportional to the distance between that point and the focus. A parabola has one directrix, similar to the focus, but ellipses and hyperbolas have two.
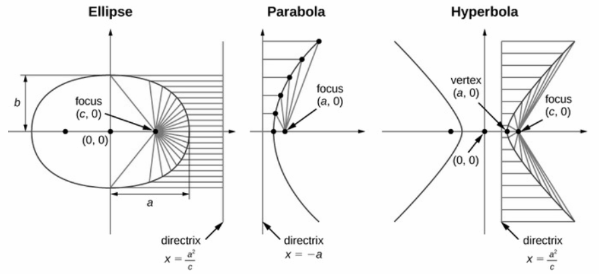
Eccentricity
Every conic section has an eccentricity parameter, indicated by the letter e. It’s a measurement of how far the conic section deviates from being circular.
The eccentricity of a conic section is calculated by dividing the distance between each point on the conic section and its focus by the perpendicular distance between that point and the nearest directrix. For any conic section, the value of e remains constant. This characteristic can be utilized to define conic sections in general. The kind of conic section can also be determined by the value of e:
- If e < 1, it is an ellipse
- If e = 1, it is a parabola
- If e > 1, it is a hyperbola
A circle’s eccentricity is zero. Two conic sections are identically shaped if and only if their eccentricities are the same.
Ellipse
The ellipse is one among the conic sections that’s produced, when a plane cuts the cone at an angle with the bottom. All circles are a particular case of the ellipse since the definition of an ellipse entails being parallel to the cone’s base. Ellipses have the following characteristics:
- Ellipse has two focal points, which are called foci.
- The fixed distance parallel to the latus rectum and perpendicular to the major axis is termed the directrix.
- The eccentricity of the ellipse lies between 0 and 1. 0 ≤ e < 1
- The total sum of each distance from the locus of an ellipse to the two focal points is constant.
- Ellipse has a major axis, a minor axis and a centre.
The Standard form of equation of ellipse is
(x-h)² / a² + (y-k)² / b² = 1
Parabola
When the plane is parallel to the cone’s surface, the plane forms a U-shaped curve. The following characteristics can be found in every parabola:
- The curve turns around at a point called Vertex, it is on the curve.
- The point which is not on the curve about which the curve bends is called the Focus.
- A line connecting the vertex and focus is known as the axis of symmetry, which divides the into two equal parts
The eccentricity value e = 1 is shared by all parabolas. Because all parabolas have the same eccentricity, they are all similar, which means that any parabola may be turned into another by changing its position and scaling. A parabola is degenerate when the plane barely touches the outside surface of the cone, indicating that it is tangent to the cone. Out of the cone’s diagonal, a straight line intersection results. Non-degenerate Parabolas can be represented using quadratic equations.f(x)=x².
Hyperbola
When a plane is parallel to the central axis of a cone, it touches both halves of the double cone, forming a hyperbola. Hyperbolas have two branches as well as the following characteristics:
- Asymptote lines are two linear graphs that the hyperbola’s curve approaches but never touches.
- The intersection of the asymptotes forms a centre.
- Each of the two branches bends around two focal points.
- Each branch has two vertices.
The Standard form of equation of Hyperbola is
(x-h)² / a² – (y-k)² / b² = 1
A hyperbola’s eccentricity is constrained to e > 1 and has no upper bound. When the eccentricity is allowed to reach +∞, the hyperbola degenerates into a straight line, which is one of its degenerate examples. A hyperbola’s other degenerate situation is to become its two straight-line asymptotes. When the plane intersects the apex of the double cone, this occurs.
Applications of Conic Sections
Many fields of study use conic sections, particularly to describe shapes. They’re used in astronomy to explain the shapes of objects’ orbits in space, for example. Two large objects in space can move in conic section orbits when they interact according to Newton’s law of universal gravitation. Depending on their qualities, they could follow ellipses, parabolas, or hyperbolas.
Conclusion
A ‘conic’ curve is one that is created by crossing a right circular cone with a plane. In Euclidean geometry, it possesses unique features. The vertex of the cone separates the conic section into two nappes, the upper nappe and the lower nappe. A conic section is a locus of a point P travelling in the plane of a fixed point F known as focus and a fixed line d known as directrix (with the focus not on d) in such a way that the ratio of point P’s distance from focus F to its distance from d is a constant e known as eccentricity.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out





