Profile
Settings
Refer your friends
Sign out
R.H.S. and S.S.S. Congruency rule
The measurements of the sides and angles of the triangles determine congruence between them. There are a few ways that can be used to verify whether any two given triangles are congruent or not. The congruence of triangles defines the given triangle and the mirror image of the triangle.
The S.S.S congruency rule state that the triangles are congruent if three sides of one triangle are equal to the other triangle. The R.H.S. congruency rule state that right triangles are congruent if the triangle’s hypotenuse and one side of the triangle are the same as the other triangle’s hypotenuse and side.
Congruence of Triangle: Overview
The word congruency means that the two given triangles have the same size and shape and both triangles can be superimposed on one another. A triangle’s position or appearance appears will change when it is rotated, reflected, or translated. The six parts of a triangle and their equal parts in the opposite triangle should be identified in this case. Two triangles are congruent if all their three angles and three sides are equal to one another.
Let there be two triangles ABC and PQR
In ΔABC and ΔPQR, as shown below, we can identify that AC=PR, CB=RQ, and BA=QP and ∠A=∠P,∠C=∠R , and ∠B=∠Q
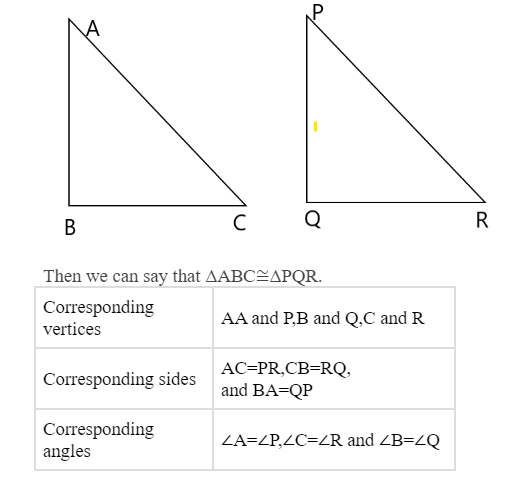
We can clearly see that △ABC≅△PQR by identifying the corresponding parts of the given triangles.
What is CPCT?
When we study the congruent triangle, we mostly cross the word CPCT. The word CPCT is short for “Corresponding Parts of Congruent Triangles.” We know, that the matching parts of all the congruent triangles are equal or the same. We typically use the abbreviation CPCT in short form instead of the full form while dealing with congruent triangle concepts and solving problems.
Conditions for Congruence of Two Triangles:
If any two triangles are of the same size and shape, they are said to be congruent. It is unnecessary to find all six corresponding elements of both triangles to be equal to determine that the given triangles are congruent. There are five conditions for any two triangles to be congruent. The basic congruence properties are S.S.S., S.A.S., A.S.A., A.A.S., and R.H.S.
Congruence Rules:
Any two triangles are congruent if they satisfy any of the five congruence rules/conditions given below.
- Side-Side-Side (S.S.S.): The triangles are congruent if all three sides of one triangle are equal to the other triangle. It is also called SSS congruency.
- Side-Angle-Side (S.A.S.): The triangles are congruent if two sides and the included angle in between those sides of the first triangle are equal to two sides and the included angle of the second triangle. It is also called SAS congruency.
- Angle-Side-Angle (A.S.A.): The triangles are congruent if two angles and the included side between those angles of the first triangle are equal to two angles and the included side of the second triangle. It is also called ASA congruency.
- Angle-Angle-Side (A.A.S.): The triangles are congruent if two angles and a non-included side of one triangle are the same as two angles and a non-included side of another triangle. It is even called AAS congruency.
- Right-Angle-Hypotenuse-Side (R.H.S.): Two right triangles are congruent if the triangle’s hypotenuse and one side are the same as the other triangle’s hypotenuse and side. It is also called RHS congruency.
SSS Rule of Congruence:
The S.S.S. criterion stands for side-by-side congruence.
Statement: If all three sides of the triangle are equal to the three equal sides of the other triangle, the two triangles are said to be congruent according to the same criterion.
Let there be two triangles which are triangle ABC and triangle YZX
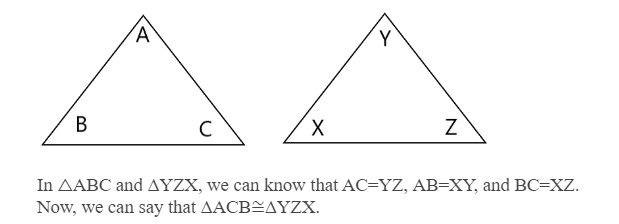
R.H.S. Congruency Rule:
Statement: The R.H.S. congruence theorem states that if the right-angled triangle’s hypotenuse and one side of the triangle are equal to the other triangle’s hypotenuse and corresponding side, then the two given triangles are said to be congruent.
Only right-angled triangles are subject to this rule, this rule doesn’t apply to any other kind of triangle.
Please note that if we keep the hypotenuse and any of the other two sides of two right triangles equal, we’ll automatically get three sides as the same because all three sides of a right triangle are related to each other, known as the Pythagoras theorem.
hypotenuse²=base²+perpendicular²
Conclusion
Here, we have discussed the congruency of RHS and SSS congruency rules. We have talked about each and every condition of congruency like SAS, AAS, SSS, and RHS. We have talked about the conditions for various congruency in detail.
