Profile
Settings
Refer your friends
Sign out
The conditional statement is a part of mathematical reasoning which is a critical skill that enables students to analyze a given hypothesis without any reference to a particular context or meaning of the particular scenario. In layman’s words, when a scientific inquiry or statement is examined, the reasoning is not based on only a scientist’s individual opinion.
Mathematical critical thinking and logical reasoning are important skills that are required to solve most math reasoning questions.
What Is Meant By a Conditional Statement?
If a statement is in the form “If p, then q” (reasoning statement) is a conditional statement. Here p ‘refers to ‘hypothesis’ and ‘q’ refers to ‘conclusion or reasoning.
For example, let us take a sentence, “If Cliff is thirsty, then she drinks water.” This is a conditional statement.
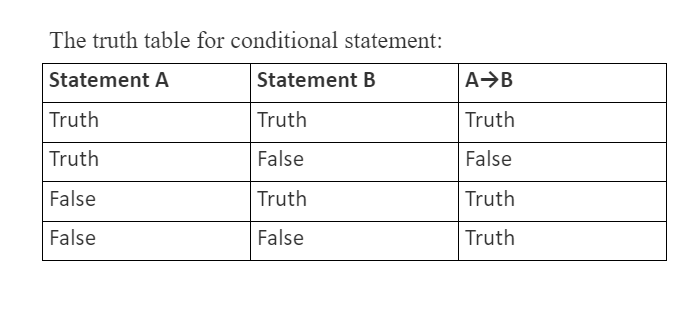
‘→’ is the symbol used to represent a relation between two statements. For example, A→B is known as the logical connector between A and B and It can be read as A implies B.
Here are a few more conditional statement examples
Example 1: If a number is divisible by 4, then it is also divisible by 2.
Example 2: If today is Monday, then tomorrow will be Tuesday.
What Are the Parts of a Conditional Statement?
Hypothesis (if) and Conclusion (then) are the two main parts that form any conditional statement.
Let us consider the above example to understand the parts of a conditional statement.
Conditional Statement: If today is Monday, then the day after tomorrow will be Wednesday.
Hypothesis: “If today is Monday.”
Conclusion: “Then the day after tomorrow will be Wednesday.”
On interchanging the form of statement the relationship between it also gets changed.
To check whether the statement is true or false, we have subsequent parts of the conditional statement. They are as follows:
- Converse
- Inverse
- Contrapositive
- Biconditional Statement
Let us consider hypothesis as statement A and Conclusion or reasoning as statement B.
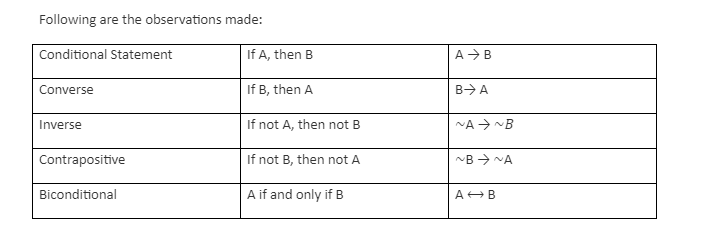
The converse of Statement-
When hypothesis and conclusion are interchanged, it is known as a converse statement.
For example,
Conditional Statement: “If today is Wednesday, then the day before yesterday was Monday.”
Hypothesis: “If today is Tuesday”
Converse: “If the day before yesterday was Monday, then today is Wednesday.”
The inverse of Statement-
When both the hypothesis and conclusion of the conditional statement are negative, it is termed an inverse of the statement.
For example,
Conditional Statement: “If today is Wednesday, then the day before yesterday was Monday”.
Inverse: “If today is not Wednesday, then the day before yesterday was not Monday.”
The conditional statement logic is, If not A, then not B as well (~A → ~B)
Contrapositive Statement-
When the hypothesis and conclusion or reasoning are negative and simultaneously interchanged, then the statement is contrapositive.
For example,
Contrapositive: “If the day before yesterday was not Monday, then today is not Wednesday”
Here the conditional statement logic is, if not B, then not A either (~B → ~A)
Biconditional Statement
The statement is a biconditional statement when a statement satisfies both the conditions to be true, being conditional and converse at the same time.
For example:
Biconditional: “Today is Wednesday if and only if the day before yesterday was Monday.”
Boolean Expression
A Boolean expression and conditional statement have some similarities. A logical statement that results in a boolean value, either be True or False, is known as a boolean expression. Sometimes, synonyms are also used to express statements such as ‘Yes’ for ‘True’ and ‘No’ for ‘False’, and also, 1 and 0 are used for digital circuits for True and False, respectively.
Boolean expressions are the statements that mostly use logical operators, i.e., AND, OR, XOR, and NOT. Therefore, if we write X AND Y = True, then it is a boolean expression.
Conclusion:
The conditional statement is a part of mathematical reasoning which is a critical skill that enables students to analyze a given hypothesis without any reference to a particular context or meaning of the particular scenario. In layman’s words, when a scientific inquiry or statement is examined, the reasoning is not based on only a scientist’s individual opinion.
