Profile
Settings
Refer your friends
Sign out
Three or more lines in a plane that go through the same point are called concurrent lines. A point of intersection is formed whenever two non-parallel lines meet. These three lines are considered to be concurrent when a third line likewise passes through the point of junction formed by the first two lines. For instance, we may observe that three heights painted on a triangle intersect at a place called the ‘Orthocenter.’ Because nonparallel lines continue endlessly and intersect at a point, only non-parallel lines have a point of concurrence.
The set of lines that meet at a common point is known as concurrent lines. To be considered concurrent lines, three or more lines must meet at some point. Only lines can be concurrent; rays and line segments cannot be concurrent since they do not always meet at the same spot. A point can have more than two lines which are passing through it. The diameters of a circle are congruent at the circle’s centre, for example. The line segments connecting the midpoints of opposite sides and the diagonals are contemporaneous in quadrilaterals.
How to find if lines are concurrent?
There are two approaches for determining if three lines are concurrent. Let’s talk about both of them.
Method 1:
Consider the following three lines:
Line 1 = a1x + b1y + c1z = 0,
Line 2 = a2x + b2y + c2z = 0, and
Line 3 = a3x + b3y + c3z = 0.
To finish, if the three lines above are parallel, the determinant indicated below should be set to 0.
Method 2: To see if three lines are concurrent, find the place of the junction of two lines and then examine if the third line goes through it. This will ensure that all three lines are active at the same time. Let us use an example to better grasp this. The following are the equations for any three lines.
4x-2y-4 = 0 ——- (1)
y = x + 2 ——- (2)
2x + 3y = 26 ——- (3)
Step 1: Using the substitution method, solve equations (1) and (2) to identify the place of intersection of lines 1 and 2.
Equation (1) is solved by substituting the value of ‘y’ from equation (2).
4x-2(x + 2)-4 = 0
4x-2x-4-4 = 0
2x – 8 = 0
x = 8/2
x = 4.
We acquire the value of ‘y’ by substituting the value of ‘x = 4’ in equation (2).
y = x + 2 ——- (2)
y = 4 + 2
y = 6
As a result, lines 1 and line 2 cross at a point (4,6).
Step 2: In the equation for the third line, substitute the point of intersection of the first two lines.
The third line’s equation is 2x + 3y = 26 ——(3)
We get 2(4) + 3(6) = 26
8 + 18 = 26
26 = 26 by substituting the values of (4,6) in equation (3).
As a result, the point of intersection coincides with the third line equation, indicating that the three lines overlap and are concurrent.
Concurrent line segment and rays:
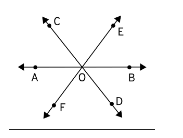
Concurrent line segments are defined as three or more line segments that meet at a single place. See the illustration below, where AB, CD, and EF are three line segments that overlap at point O. As a result, we can apply concurrency to line segments as well.
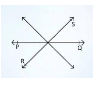
Concurrent Rays are formed when three or more Rays in a two-dimensional plane intersect or meet at a single place. For all the beams, the single point is the point of convergence. Three rays PQ, and RS intersect at point O and are parallel to each other in the diagram below.
Conclusion:
Three or more lines in a plane that go through the same point are called concurrent lines. A point of intersection is formed whenever two non-parallel lines meet. Concurrent lines are three or more lines in a plane that passes through the same point. These three lines are considered to be concurrent when a third line likewise passes through the point of junction formed by the first two lines.
The set of lines that meet at a common point is known as concurrent lines. To be considered concurrent lines, three or more lines must meet at some point.
The diameters of a circle are congruent at the circle’s centre, for example. The line segments connecting the midpoints of opposite sides and the diagonals are contemporaneous in quadrilaterals.
