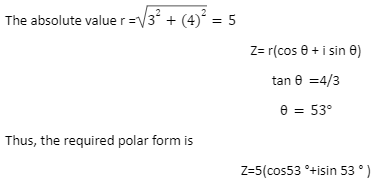Watch Free Classes

We know that the square root of 4 is 2 but we cannot calculate the square root of -4 and from here a new concept generates and that leads to the new concept in mathematics that is a complex number.

Definition

It is the sum of a real number and an imaginary number and is of the form of a + ib which is usually represented by Z.

In Mathematics, a complex Number is an algebraic expression that includes the factor 

i = √(-1).

And “i” is called an iota.

A complex number are of the form Z=a=ib,  has two parts,

  • Real part: The real part of given Z is “a” and is denoted by Re(Z)=a.

  • Imaginary Part.: The imaginary part of given Z is “b” and is denoted by Im(Z)=b

Addition of complex numbers

Let us take two complex numbers to say,

 z1 = a + ib and  z2 = c + id,

Then the sum of these two complex numbers is:

z1+ z2 = (a + ib) + (c + id)

=(a + c) + i(b + d)

Therefore, 

z1 + z2 = Re (z1+ z2) + Im(z1+ z2)

Difference of complex numbers

Let us take two complex numbers to say,

 z1= a + ib and  z2 = c + id, 

Then the difference of these two complex numbers is:

z1- z2= (a + ib) – (c + id)

= (a – c) + i (b – d)

Therefore, 

z1 – z2 = Re(z1 – z2 ) + Im(z1 – z2)

Note:

  • Pure Real Number: When the imaginary part of the complex number is Zero(0) 

Example: 4, 8, 5 etc

  • Pure Imaginary Number: When the real part of the complex number is Zero(0)

Example: 4i, 9i, 10i etc

  • The addition of complex numbers can be another complex number.

  • The subtraction of complex numbers can be another complex number.

Roots of Complex Number

Follow the simple two-step to find the roots of the complex number

  1. Convert the given Complex number in the Polar form.

Let us take a complex number Z=a+ib

Now, convert this into the polar form we get,

Z= r(cos + i sin )

  1. Solve by Applying De Moivre’s Theorem.

For any Complex Number Z and any integer n, 

rcos +isin n=rn(cos n +isin n )

Conclusion

A complex number is a number that has two real parts and an imaginary part. A complex number can also be converted into polar form, [Z=a+ib= r (cos + i sin )] and the root of the complex number can be calculated by first converting the complex number into its polar form and then applying De Moivre’s Theorem.