Comparison Between Rolle’s Theorem and Lagrange’s Mean Value Theorem

Mean Value Theorems (MVT) are a common occurrence in the literature on mathematics education. It is one of the most significant techniques in differential and integral calculus for proving a variety of other theorems. Rolle’s theorem, a specific case, is sometimes taught with it. Michel Rolle (1652-1719), a French mathematician who devised the now-common notation for the nth root and claimed that -a > -b, for positive a and b, a b, proved Rolle’s theorem. The achievement went against Descartes’ teachings and paved the way for the widespread use of the number line. Rolle’s Theorem is a variant of the mean value theorem that meets specific requirements. Lagrange’s mean value theorem is both the mean value theorem and the first mean value theorem at the same time. The average of the provided values can be understood as the mean. The procedure of determining the mean value of two separate functions is different in integrals. Let’s look at Rolle’s theorem, as well as the mean value and geometrical meaning of such functions.

Lagrange’s Mean Value Theorem

If a function f exists on the closed interval [a,b] and meets the following criteria –

I.) On the interval [a, b], the function f is continuous.

ii)On the interval, the function f is differentiable (a, b)

Then there is a value x = c that is such that

f'(c) = [f(b) – f(a)] / (b-a)

The first mean value theorem, or Lagrange’s mean value theorem, is another name for this theorem.

Theorem of Rolle

Rolle’s Theorem is a specific example of Lagrange’s mean value theorem, which says that:

If a function f is defined in the interval [a, b] such that it meets the following requirements.

i) On the interval [a, b], the function f is continuous.

ii) On the open interval, the function f is differentiable (a, b)

iii) If f (a) = f (b), then there must be at least one value of x. Let us assume that this value is c, which sits between a and b, i.e. (a c b), with f'(c) = 0.

If a function is continuous on the closed interval [a, b] and differentiable on the open interval, it is said to be continuous (a, b) Then in (a, b), there is a point x = c where f'(c) = 0.

Rolle’s Theorem is given a geometric explanation.

Theorem of Rolle

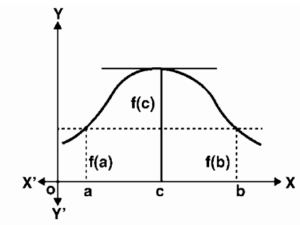
There is at least one tangent to the curve that is parallel to the x-axis if the curve y = f(x) is continuous between x = a and x = b, and a tangent can be drawn at any point inside this interval, and the ordinates corresponding to the abscissa and are similar.

If f (x) is a polynomial function in x and the two roots of the equation f(x) = 0 are x = a and x = b, then at least one root of the equation f'(x) = 0 between these two values, according to this theorem. The inverse of Rolle’s theorem is false; there may be more than one value of x for which the theorem stands true, but there is a good chance that only one such value exists.

Statement of Rolle’s Theorem

Rolle’s theorem can be expressed mathematically as:

Let f: [a, b] R be continuous on interval [a, b] and differentiable on interval (a, b), with f(a) = f(b). Then some c in (a, b) exists such that f′(c) = 0.

Example of the Rolle’s Theorem:

For the functions y = x2 + 2, a = –2, and b = 2, prove Rolle’s theorem.

Solution:

The function y = x2 + 2 is continuous in [– 2, 2] and differentiable in (– 2, 2), according to Rolle’s theorem.

Given the circumstances,

f(x) = x² + 2

f (-2) = (-2)² + 2 = 4 + 2 = 6

f (2) = (2)² + 2 = 4 + 2= 6

Hence, f (– 2) = f (2) = 6

As a result, the values of f(x) at –2 and 2 are the same.

Now, f'(x) = 2x

According to Rolle’s theorem, there is a point c (– 2, 2) where f′(c) = 0.

f′(c) = 2(0) = 0 at c = 0, when c = 0 (− 2, 2)

As a result, it has been confirmed.

This is everything about Rolle’s theorem and the mean value theorem.

Conclusion

The study of algebraic equations has resulted in two fundamental statements in the theory of functions:

1. The root interval theorem
2. A derivative’s root theorem

The result was the Mean Value Theorem.

Several authors refer to the “Theorem of root interval” as “Second Rolle’s Theorem” or “Theorem of Bolzano Cauchy” in Russian literature.

It took roughly 300 years for Rolle’s Theorem to reach its ultimate form. It has a huge impact on differential geometry, functional analysis, mechanics, and other fields.

“Theoretical evolution of differential and integral calculus is based on this theorem.”