Definition:
Combination is a mathematical approach for estimating the number of possible arrangements in a set of objects when the order of the elements does not matter. You can mix and match the components in any order you like. Permutations and combinations are often mistaken.
Introduction:
Selections are another term for combinations. Combinations refer to the selecting of items from a set of options. We have no intention of arranging things here.We plan to choose them.The number of distinct r-selections or combinations out of a set of n objects is denoted by the symbol ⁿcr
Arrangements and permutations are not the same as combinations. With the help of examples and FAQs, we’ll learn more about how to calculate combinations, the combinations formula, and the differences between permutation and combinations.
A permutation is a certain order in which items are arranged.Set members or elements are arranged in a linear or sequential order here.
Combination and Permutation formula:
The combinations formula is used to quickly calculate the number of various groups of r objects that can be constructed from the n different objects that are available. The factorial of n divided by the product of the factorials of r and the factorial of the difference of n and r, respectively, is the formula for combinations.

- We need to understand the concept of factorial to use the combinations formula, and we have
n! = 1 23…. (n-1) n.
The general permutation formula is as follows:

Permutation can be classified into two types:
- Repetition is permitted
- There will be no repetition, such as the first three people in a running race.You can’t be first and second at the same time.
Combinations are calculated by using the combinations formula, as well as factorials and permutations.
In general, imagine we have n items at our disposal and then we wish to determine the number of ways we can choose r items from these n items. We begin by calculating the total number of permutations of these n items taken r at a time. ⁿPr would be that number.Since r objects can be permuted among themselves in r! ways, each combination in this list of ⁿPr permutations will be counted r! times.As a result, ⁿcr denotes the total number of permutations and combinations of these n items, taken r at a time.the following will be:
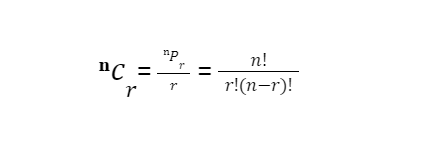
Example on Combinations:
Take a look at the term EDUCATION.There are nine different letters in this word.With the letters in this word, how many 3-letter permutations (words) may be formed? We now know how to respond to inquiries like this; in this case, the answer will be 9P3.
Consider the following three-letter combinations derived from the letters A, E, and T in the word EDUCATION:
AET , ATE, EAT, ETA, TAE, TEA
These six distinct layouts all correspond to the same set of letters: A, E, and T.
As a result, each unique Combination corresponds to six possible arrangements in the list of all 3-letter permutations.We divide the number of 3-letter permutations by 6 to get the number of distinct 3-letter options.
As a result, the total number of 3-letter choices will be P (9,3) ⁄ 6 = 60480 ⁄ 6 = 10,080
Difference between Combination and Permutation:
What exactly do permutations and combinations indicate?A permutation is the process of putting things or numbers in a particular order.Combinations are a method of picking things or numbers from a set of objects or a collection without regard for their order.
We use the word “combination” casually in English, as though the order of things isn’t significant.To put it another way:
- “I made a fruit salad with apples, grapes, and bananas.” It doesn’t matter what sequence the fruits are in; “bananas, grapes, and apples” or “grapes, apples, and bananas” are both acceptable.
- “The safe’s combination is 472.”We are now concerned about the order.”724” and “247” will not work.It has to be 4-7-2 precisely.
As a result, we use more strong language in mathematics:
- It is a Combination when the sequence doesn’t matter.
- It’s a Permutation when the order matters.
Combination of Functions:
Sums, differences, products, and quotients can be used to combine two functions to generate new ones.
All real numbers that are common to the domains of f and g make up the domain of an arithmetic combination of functions f and g.
While mathematical combinations of functions are simple and obvious, a composition is a different type of combination.
It is simple to find the sum, difference, product, or quotient of functions.
Sum
(f + g)(x) = f(x) + g(x)
Difference
(f – g)(x) = f(x) – g(x)
Product
(f · g)(x) = f(x) · g(x)
Quotient
As long as g(x) is not zero, quotient (f / g)(x)= f(x) / g(x).
The application of one function to another is referred to as a function composition.A tiny circle between the function names is the sign for function composition.Because I can’t perform that sign in text mode on the web, I’ll symbolize function composition with a lower case oh “o.”
- (fog)(x) = f [g(x)]
- (gof)(x) = g[f(x)]
“If composed with g of x” and “g composed with f of x” should be interpreted as “f composed with g of x” and “g composed with f of x,” respectively.
The functions on the outside are always written first, followed by the functions on the inside.The sequence is essential.Function composition is not commutative.
Important Notes:
- Consider the phrase “number of options” whenever you hear the phrase “number of combinations.”It doesn’t matter what order the objects are in when you’re picking them.XYZ and XZY, for example, are two distinct arrangements with the same selection.

 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






