Circumcenter of a Triangle

The Circumcenter is the place where the perpendicular bisectors of a triangle intersect. It is found on the inside of an acute triangle, on the outside of an obtuse triangle, and at the centre of the hypotenuse of a right triangle.

The line or ray that splits another line segment into two equal halves at 900 is known as a perpendicular bisector. The hypotenuse, or side opposite the right angle, is the longest side of a right-angled triangle. The circumcenter of a polygon is the centre of the circumcircle drawn around it. The circumcenter of a polygon is the circle that goes through all of its vertices, and the circumcircle is the circle that passes through all of its vertices. Cyclic polygons are all polygons that have circumcircles. A circumcircle is not required for all polygons.

Circumcenter of a triangle

The point of intersection of three perpendicular lines from the triangle’s sides is called the circumcenter. The point of intersection is also known as the concurrency point.

Circumcenter of a triangle properties

• The triangle’s vertices are all equal from the circumcenter. Take a look at the image below to get a better idea of what I’m talking about. Connect O to the triangle’s vertices. 

AO = BO = CO As a result, the triangle’s vertices are equidistant from the circumcenter.

• Isosceles triangles are all the new triangles generated by attaching O to the vertices.

• When A is acute or when O and A are on the same side of BC, ∠BOC = 2 ∠A 

• When A is obtuse or O and A are on opposite sides of BC, ∠BOC = 2( 180° – ∠A) 

• Varied types of triangles have different circumcenter locations.

Constructing the Triangle’s Circumcenter

We use a geometric instrument called a compass to find the circumcenter of a triangle. The compass is made up of two ends, one of which is positioned on the triangle’s hypotenuse and the other on the triangle’s vertex. The processes for making a triangle’s circumcenter are as follows:

1. Using a compass, draw the perpendicular bisectors of all the triangle’s sides.

2. Extend each of the perpendicular bisectors to a point. The circumcenter is marked by the letter O at the junction location.

3. Draw a circle using a compass, with O as the centre and any vertex of the triangle as a point on the circumference; this circle is our circumcircle, with O as the centre.

How to Calculate a Triangle’s Circumcenter

To find the circumcenter of a triangle, follow these steps:

• Calculate the midpoint of given coordinates, such as the AB, AC, and BC midpoints.

• Calculate the slope of the line in question.

• Find the equation of the line (y-y1) = m using the midpoint and slope (x-x1)

• Find the equation for the opposite line in the same way.

• Find the intersection point of two bisector equations to solve them.

• The circumcenter of the supplied triangle will be the calculated intersection point.

Circumcenter formula

A = (x1,y1), B = (x2,y2),  and C = (x3,y3), are the triangle ABC’s vertices, and A,B,C are the respective angles

Then,

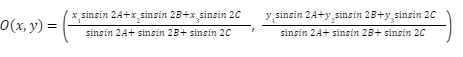
How to find the circumcenter of a triangle given 3 points

Example: A = (2,1), B = (-2, 3), and C = (1, -2) are the given points 

We must solve any two bisector equations and find the intersection locations to determine the circumcentre.

As a result, AB’s midpoint = (0,2)

AB’s slope is -1/2.

The negative reciprocal of the given slope is the bisector’s slope.

As the perpendicular bisector’s slope is 2, the equation for the perpendicular bisector of AB is

y=2x+2…….(1)

AC’s midpoint = (3/2,-1/2)

AC’s Slope = 3

The negative reciprocal of the given slope is the bisector’s slope.

As the perpendicular bisector’s slope is -1/3, the equation for the perpendicular bisector of AC is

x+3y=0 …..(2)

1 & 2 equations must be solved

we obtain,

y=2/7 and x=-6/7

As a result, the circumcentre is (-6/7,2/7).

Conclusion

In this article we learn, the circumcenter is the circumcircle’s centre. A triangle’s vertices are all equidistant from the circumcenter. The circumcenter of an acute-angled triangle is located within the triangle. It is located on the outside of an obtuse-angled triangle. We’d have to find the circumcenter in order to pinpoint the exact position of the hospital. The circumcenter is the place where all of a triangle’s perpendicular bisectors meet. Line segments, or lines, that bisect another line to form right angles are known as perpendicular bisectors.