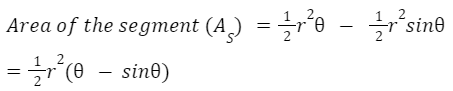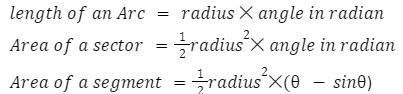Angle measurement is the basis of trigonometry. The circular system of angle measurement is one of the most useful systems to determine the measurements of angles. These are measured in the circulatory system in terms of radian, which is the S.I unit of angles. In this article, we shall shed light upon the concept of a circular system of angle measurement. We will learn how to convert angles in the degree to radian and vice versa. We will also look through the calculation of the length of an arc, areas of sectors and segments. So, let us begin with the topic.
Concept of angles – How to measure it?
When two straight lines intersect each other in a plane, there is a space between them close to the intersecting point; that space is called an angle. Now we have a quantity; we have to measure it. Measuring an angle can be done by using three systems, i.e.
- British System or Sexagesimal System,
- French System or Centesimal System,
- Circular System or Radian Measure.
We shall discuss the circular system of angle measurement here.
Circular system of Angle Measurement meaning: Radian measure
If we consider a circle with a radius of 1 unit, then take a sector so that the arc also measures 1 unit. There is an angle between the two radii holding that sector. That very angle
From this knowledge, we can solve the circular system of angle measurement examples.
Relation between radians and arc length
Take any circle of any radius (r). Now take any arc (l ) on that circle. If that angle (θ) subtended by that arc is measured in radian, it will be the ratio of the length of arc and radius.
From the above example, we can see that if the length of radius and arc is same, then the angle subtended at the centre is one radian (1c).
Alternative definition of radian: One radian (1c) is the ratio of arc and radius of the same length.
Relation between radians and sector area
The enclosed 2D geometrical shape formed by two radii and an arc is called a sector.
Relation between radians and segment area
If we take an arc and join its endpoints, we find a chord. Now, the enclosed 2D geometrical shape formed by the arc and the chord is called a segment.
Conclusion
Roger Cotes gave the concept of radian in 1714. He didn’t coin the name ‘radian’. The name was most probably coined by James Thomson. But, the circular system of angle measurement has been used by mathematicians since early 1400. They used diameter parts as a unit of this primitive form of the circulatory system of angle measurement. Trigonometry and the polar coordinate systems are the two most prominent fields where this system is used. Below we shall discuss some frequently asked questions and some circular system of angle measurement examples.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out