Profile
Settings
Refer your friends
Sign out
The point of concurrence of all the three medians is simply known as the centroid of that triangle. In order to understand centroid, we will first go through the concept of median. Median is simply a line segment which is drawn from any vertex of a triangle to the midpoint of the opposite side of that vertex. Since a median joins the midpoint, it also divides the triangle into 2 equal parts. Let’s have a look below
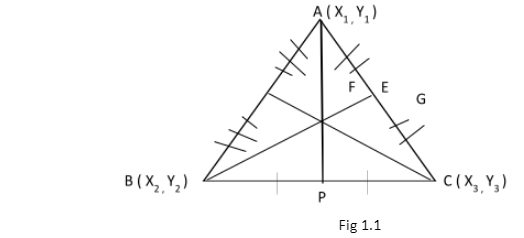
In ΔABC, P is the midpoint of BC. The line segment originating from A and joining BC is the median. Similarly, CF and BE are medians too and G is the point of concurrence of all the three medians which is known as Centroid. Let’s have a look at it’s properties, formula and some examples.
Properties of Centroid
- Centroid divides the median into 2:1 ratio
- Centroid is also known as geometric centre of the triangle
- Centroid always lies within the triangle
- Centroid is the most widely used point of concurrency among the other points of concurrency like circumcentre, incentre, orthocentre.
Formula to find Centroid
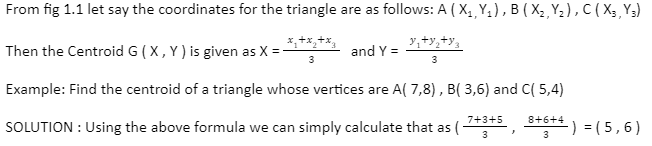
Centroid theorem
BG = 15 cm
We know that median as well as altitude is one and the same for equilateral triangles. Using Pythagoras theorem, we can find altitude = median as 302–152=900-225=675
and from the above theorem AG = 2/3 of 675.
Relation between orthocentre, centroid and circumcentre
- A line segment produced from one vertex to the other side of a triangle and which is perpendicular to that side is known as altitude. The point of concurrence of altitudes is known as Orthocentre
- The perpendicular bisector of a triangle is the line drawn from the midpoint of the triangle and the point of concurrence is known as circumcentre
- Centroid as stated above is concurrence of the medians
Readers must refer in detail to the properties of orthocentre and circumcentre.
Examples
- If the centroid of a triangle formed by (8, x), (y, -10) and (14,16) is (6,10), then the values of x and y are?
Solution: We know that (8+y+14)/3 = 6
22+y = 18
Y = -4
Likewise (x +(-10) +16)/3 = 10
X -10 +16 = 30
X = 40-16 = 24
So, value of x and y are 24 and -4 respectively
Conclusion
We very well conclude that intersection of the medians is simply known as the Centroid of triangle. Centroid divides the median into the ratio of 2:1. Centroids can never lie outside the triangle; it always lies inside the triangle. Centroid property is the most commonly and widely used concurrency property. Readers must take note of other properties like orthocentre, incentre, circumcentre etc. In this article we worked with the centroid of a triangle; other polygons have analogous interpretations of the centroid; it acts as the centre of mass of the vertices of the polygon.
