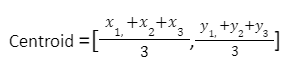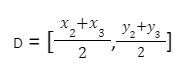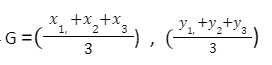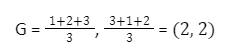Centroid

The centroid is the geometric centre of a two-dimensional plane surface in mathematics. It’s a point that’s found by calculating the arithmetic mean of all the points on a plane surface. It is defined as the average of all the points in the planar figure if not otherwise specified. For several geometrical shapes, the centroid can be found. In physics and engineering, centroids are most useful for understanding centres of gravity and moments of inertia. Only irregular geometries with extended sides have centres of gravity on the outside, therefore it appears natural that the centroid should remain within the triangle. The medians are straight lines that run from one vertex to the other, splitting the opposing side into two equal halves. The triangle is also divided into smaller triangles with equal sizes by a middle. There are four points of concurrency in a triangle, namely: Orthocentre, Incentre, Circumcentre & Centroid.

Centroid definition 

“The centroid or geometric centre of a flat shape is the arithmetic mean position of all the points in the figure in mathematics and science. Informally, it’s the point at which a perfectly balanced cutout of the shape (with evenly distributed mass) might be balanced on the tip of a pin.”

Centroid’s Properties

• The intersection of the medians makes it.

• It is one of a triangle’s points of concurrency.

• It is always found within the triangle (together with the incenter, which is another of the triangle’s concurrent points).

• Each median is divided by the centroid in a 2:1 ratio. In other words, the centroid of any given median will always be 2/3 of the way down it.

Centroid rectangle formula

This formula is used to get the coordinates of the triangle’s centroid when the triangle’s vertices are known.

Let’s assume the vertices of a triangle’s coordinates are  (x1 , y1), (x2,y2), (x3,y3)

The formula for the triangle’s centroid is then,

where,

x1, x2,x3 are the three vertices’ x-coordinates,

y1, y2,y3 are the three vertices’ y-coordinates,

Centroid Formula Derivation

The midpoints of sides BC, AC, and AB are D, E, and F, respectively.

The coordinates of point D (midpoint of triangle side BC) can be determined using the mid-point formula of coordinate geometry:

According to the centroid theorem, the triangle’s centroid G divides any median in a ratio of 2: 1. As a result, when we use the section formula of coordinate geometry to find G’s coordinates, we get:

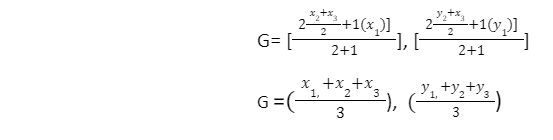
How to find the centroid of a triangle construction

Steps to Creating a Centroid

1. Make a triangle with your pencil.

2. Take a measurement of one of the triangle’s sides.

3. Make a point in the middle of one of the triangle’s sides.

4. From the middle to the opposite vertex, draw a line segment. A median is the term for the segment you just made.

5. Repeat steps 2-4 for the triangle’s remaining two sides.

6. Mark the intersection of all three medians. The centroid is this place.

Example of centroid

Find the centroid of a triangle with vertices (1,3), (2,1), and (3,2).

Solution:

To help find: the triangle’s centroid

We can determine from the centroid formula that Centroid,

Answer: G is the centroid of the given triangle (2, 2)

Conclusion

So in this article we learn, A triangle’s centroid is the place where the triangle’s three medians meet. A triangle’s median is a line segment connecting one vertex to the triangle’s midpoint on the opposite end. The triangle’s centroid is also known as the centre of gravity. In physics and engineering, centroids are most useful for understanding centres of gravity and moments of inertia. Only irregular geometries with extended sides have centres of gravity on the outside, therefore it appears natural that the centroid should remain within the triangle.