The Cartesian product of two sets A and B, designated A B, is the set of all ordered pairs (a, b) where is in A and b is in B. In mathematics, specifically set theory, the Cartesian product of two sets A and B, called A B, is the set of all ordered pairs (a, b) where an is in A and b is in B. That is, in terms of set-builder notation. Cartesian products of sets can be thought of as the ordered product of two non-empty sets. The sets’ end product will be a collection of all ordered pairs acquired by multiplying the two non-empty sets together. Two elements are chosen from each of the two sets in an ordered pair. Example: A× B = (2,x), (2,y),(3,x),(3,y) is the Cartesian product of two sets A = 2,3 and B = x,y.
Cartesian product
The term ‘product’ refers to the result of multiplying two or more values together in mathematics. For instance, 45 is the result of multiplying 9 and 5. Basic set operations such as Union and Intersection, which are done on two or more sets, must be understood. The Cartesian product is another operation that takes two sets and returns a collection of ordered pairs.
The Cartesian product of Sets A and B is defined as the collection of all ordered pairs (x, y) where x belongs to A and y belongs to B in mathematics. When A = 1, 2 and B = 3, 4, 5, the Cartesian Product of A and B is (1, 3), (1, 4), (1, 5), (2, 3), (2, 4), (2, 5).
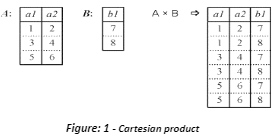
Cartesian product of sets
Any collection of objects (elements) in mathematics and logic, which may or may not be mathematical. The intuitive concept of a set is likely older than the concept of a number. For example, members of a herd of animals can be matched with stones in a sack without any of the individuals in either group being numbered. The concept goes on indefinitely for example, the set of integers from 1 to 100 is finite, whereas the set of all integers is infinite. A list of all its members contained in braces is a popular representation of a set.. A set with no members is known as an empty, or null, set, and denoted by the ∅ sign.
Or “The set of all possible ordered combinations where the first component is from A and the second component is from B is the cartesian product of two non-empty sets A and B. The resulting collection of ordered pairs is denoted by A×B.”
Eg: Let A = {1, 2} and B = {4, 5, 6} be the numbers.
A B = {(1, 4), (1, 5), (1, 6), (2, 4), (2, 5), (2, 6)}
Every ordered pair has a first component from set A and a second component from set B.
Cartesian product Properties
- The Cartesian product is non-commutative in the following ways: A × B ≠ B × A
- A × B = B × A, only if A = B
- The number of elements in A × B is defined as the cardinality of the Cartesian Product, which is equal to the product of the cardinality of both sets: |A × B| = |A| * |B|
- A × B = {∅}, if either A = {∅} or B = {∅}
Cartesian product of graphs
The box product of graphs is another name for the Cartesian product of graphs.
Because the graphs (F□G)□H an & F□(G□H) are inherently isomorphic, the operation is associative. The operation is commutative on isomorphism classes of graphs, and the graphs G□H and H□G are naturally isomorphic to a greater extent, but it is not commutative on labeled graphs.
The notation G H has long been associated with Cartesian graph products, although it is now more generally associated with a different graph construction known as the tensor product of graphs. Because it graphically depicts the four edges arising from the Cartesian product of two edges, the square symbol is an intuitive and unambiguous notation for the Cartesian product.
Conclusion
The term ‘product’ refers to the result of multiplying two or more values together in mathematics. For instance, 45 is the result of multiplying 9 and 5. Basic set operations such as Union and Intersection, which are done on two or more sets, must be understood. The Cartesian product is another operation that takes two sets and returns a collection of ordered pairs.
In computing, a Cartesian product is almost identical to a Cartesian product in mathematics. It will be useful in matrix applications. In SQL, it describes a fault in which you join two tables incorrectly and end up with numerous records from one table related to each of the entries from the other, rather than the expected one.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






