Cartesian Plane

The cartesian coordinate system includes a two-dimensional plane called the Cartesian Plane. Rene Descartes designed the cartesian plane in the 17th century. A cartesian plane’s most essential property is that it connects two branches of mathematics: Euclidean Geometry and Algebra.

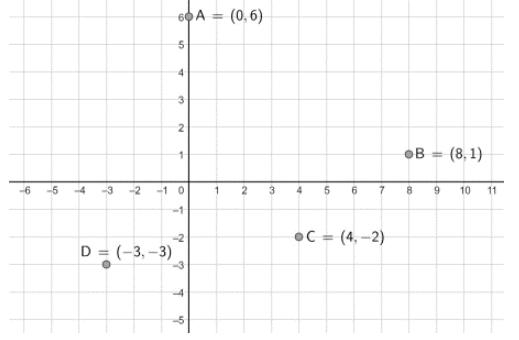
Numerical coordinates can be used to specify any point on a cartesian plane. An ordered pair is used to express the coordinates of a point on a cartesian plane. These points are also signed and are spaced at a specific distance between two perpendicular lines known as axes. The x-axis and the y-axis are the two coordinate axes that can exist in a cartesian plane. We’ll look at the definition, quadrants, and graphs of a cartesian plane in depth in this article.

Cartesian Plane

Two perpendicular number lines define a Cartesian plane: the x-axis, which is horizontal, and the y-axis, which is vertical. It is named after French mathematician Rene Descartes, who formalised its application in mathematics. We can describe any point in the plane with an ordered pair of numbers using these axes.

The Cartesian plane extends in all directions indefinitely. Maths textbooks commonly draw arrows at the ends of the axes to demonstrate this.

A point’s coordinates, a pair of numbers enclosed in parenthesis, determine its location in the plane: (x,y). The point’s horizontal position is represented by the first number x, while its vertical position is represented by the second number y. The origin is a “centre” point whose coordinates are (0,0). As indicated in the diagram, the point (5,2) is 5 units to the right of the origin and 2 units up. Negative coordinate numbers indicate that we should turn left or down. For more information, look at the other locations in the diagram.

There are four quadrants in the Cartesian plane. Starting at the upper right and working counterclockwise, these are numbered I through IV. (For some reason, everyone does this in roman numbers.)

Both the x- and y-coordinates are positive in Quadrant I; the x-coordinate is negative in Quadrant II, but the y-coordinate is positive; both are negative in Quadrant III; and x is positive but y is negative in Quadrant IV.

Points that are parallel to an axis (i.e., have at least one coordinate equal to 0) are said to be in no quadrant. The horizontal x-axis has coordinates of the type (x,0), and the vertical y-axis has coordinates of the form (0,y).

Cartesian Plane Graph Examples

A cartesian plane graph is a diagram that depicts the relationship between two variables graphically. When we have a two-variable equation, we need two axes (x and y) to graph it. The steps for graphing a two-variable equation are as follows:

• Substitute a numerical number for the value of x.

• Find the value of y that corresponds to the equivalent value of x.

• To gain a lot of test points, repeat the first two steps several times.

• To create the needed graph, connect these points.

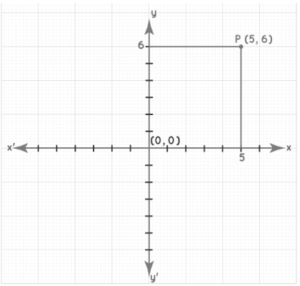
Example: The x and y axes are the intersecting horizontal and vertical lines, respectively. The coordinates of the point (5, 6) show that it is 5 units away from the y-axis and 6 units away from the x-axis.

Cartesian Plane Trigonometric Function

We used right-angled triangles to define the trigonometric ratios. These definitions can be applied to any angle, with the exception that the definitions are based solely on the size of the angle, not on the lengths of the triangle’s sides. We can find out the angle between the x-axis and that line by plotting any point on the Cartesian plane and then drawing a line from the origin to that point. We’ll look at this in detail for two specific issues before moving on to the more general scenario.

Find an Angle for Specific Point: P and Q have been plotted in the diagram below. A line is drawn from the origin (O) to each point. The dotted lines demonstrate how each point can be made into a right-angled triangle. Always draw the dotted line parallel to the x-axis. We can now calculate the angles A and B:

We can see that x=2 and y=3 from the coordinates of P(2;3). As a result, we know that the length of the side opposite A is 3 and the next side is 2. Using:

tan tan A=  opposit/adjacent = 3/2

A=56.3°

Finding any Angle: If we construct a circle with the origin (O) in its centre and passing through the point P(x;y), the distance between the origin and point P is the radius of the circle, which we represent by r. The angle produced by the line OP and the x-axis is denoted as.

All trigonometric ratios can be rewritten in terms of x, y, and r. The following are the general definitions for trigonometric ratios:

sin sin θ = y/r          cosec θ= r/y

cos cos θ  = x/r       sec sec θ = r/x

tan tan θ  = y/x       cot θ= x/y

Conclusion

A cartesian plane is defined as a plane that is formed by the intersection of two perpendicular coordinate axes. The horizontal axis is the x-axis, while the vertical axis is the y-axis. The origin, whose location is denoted by, is the point at where these axes meet (0, 0). On the cartesian plane, any point can be represented as (x, y). x represents the distance between the point and the y-axis, whereas y represents the distance between the point and the x-axis.