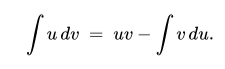Calculus is designed for a typical second or third semester general calculus course and includes innovative features that enhance student learning.
Integration by Parts:
In calculus, more generally in mathematical analysis, integration by parts is the process of finding the integral of the product of functions given the integral of the product of their derivatives and indefinite integrals. It is often used to transform an indefinite integral of a function product into an indefinite integral that makes it easier to find a solution. This rule can be thought of as an integrated version of the product rule of differentiation.
The idea of integration by parts was proposed by Brook Taylor in 1715. Brook Taylor also proposed Taylor’s famous theorem. Integrals are generally calculated for functions that have derivative expressions. Here, integration by parts is an additional technique used to find the integration of the product of functions. Converts the integral of the product of functions into an integral that makes it easy to calculate the solution.
Part integration is used to integrate products with two or more functions. The format of the two functions f (x) and g (x) to be integrated is ∫f (x). g (x). Therefore, it can be called the rule of product of integration. Of the two functions, the first function f (x) is chosen so that its derivative exists, and the second function g (x) is chosen so that the integral of such a function exists.
∫f(x). g(x). dx=f(x)∫g(x). dx−∫(f′(x)∫g(x). dx). dx+C
Integral of (1st function x 2nd function) = (1st function) x (Integral of 2nd function)-(Integral of derivative of 1st function x Integral of 2nd function). In integration by parts, the equation is split into two parts, and you can observe the integral of the derivative of the first function f (x) in the second part and the integral of the second function g (x) in both parts. For simplicity, these functions are often represented as “u” and “v”, respectively. The integration of uv expressions using the ‘u’ and ‘v’ notations is as follows:
∫udv = uv-∫vdu.
The integration by parts equation states:
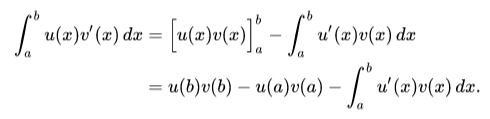
Or, if u = u (x) and du = u` (x) dx, and v = v (x) and dv = v'(x) dx, the expression can be written more compactly.
Mathematician Brook Taylor discovered integration by parts and first published the idea in 1715. The Riemann-Stieltjes and Lebesgue-Stieltjes integrals have a more general integration by parts formulation. The discrete analog of the sequence is called summation by parts.
Integration By Parts Formula:
The integration by parts formula is used to find the integral of the product of two different types of functions. B. Logarithms, inverse trigonometric functions, algebra, trigonometric functions, and exponential functions. Integration by parts formulas is used to find the integral of a product. Product Differentiation Rules allow you to choose uv, u (x), v (x) in any order. But when using integration by parts, to select the first function u (x), check which of the following functions comes first in the following order, then call it You have to look.
- Logarithmic (L)
- Inverse trigonometric (I)
- Algebraic (A)
- Trigonometric (T)
- Exponential (E)
This can be confirmed in the LIATE rule. Note that this order can also be ILATE. For example, if you need to find ∫ x ln x dx (x is an algebraic function, ln is a logarithmic function), select lnx equal to u (x) because LIATE displays the logarithmic function before the algebraic function. increase. The integration by parts formula is defined in two ways. You can use both to integrate the product of the two functions.
Integration By Parts Formula Derivation:
The proof of integration by parts is obtained from the equation of the derivative of the product of the two functions. For two functions f (x) and g (x), the derivative of the product of these two functions is the derivative of the first function multiplied by the second function and the derivative of the second function. First function.
Let’s use the product rule of differentiation to derive the equation for integration by parts. Consider two functions u and v. Their product is y. That is, applying the y = uv product differentiation rule yields
d / dx (uv) = u (dv / dx) + v (du / dx)
. Sort the terms here.
u (dv / dx) = d / dx (uv) v (du / dx) Integral on both sides for
x,
∫u (dv / dx) (dx) = ∫d / dx (uv) dx ∫v (du / dx) If you remove the dx
term,
∫ udv = uv -∫ vdu
, which gives you the integration by parts equation.
Applications of Integration by Parts:
This integral formula applies to functions or formulas that do not have an integral formula. Here, we try to derive the integral by partially incorporating this integral formula. Logarithmic and inverse trigonometric functions have no integer answer. Let’s find out by integration log x and tan-1x.
Integration of Logarithmic Function:
∫ log x. dx = ∫ logx.1. dx
= log x. ∫1. dx – ∫ ((log x)’. ∫ 1. dx). dx
=logx.x -∫ (1/x .x). dx
=x log x – ∫ 1.dx
=x log x – x + C
Integration of Inverse Trigonometric Function:
∫ tan-1x. dx = ∫tan-1x.1.dx
= tan-1x.∫1.dx – ∫((tan-1x)’. ∫ 1. dx). dx
= tan-1x. x – ∫ (1/ (1 + x²).x). dx
= x. tan-1x – ∫ 2x/ (2(1 + x²)). dx
= x. tan-1x – ½.log (1 + x²) + C
Conclusion:
Integration by parts is a technique for performing an indefinite integral ∫ udv or a constant integral ∫ udv by expanding the derivative of the product of the function d (uv) and expressing the original integral with the known integral ∫ udv.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out