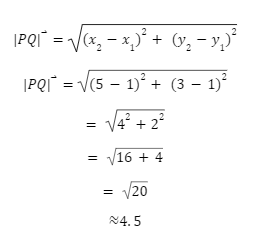Calculate Vector Product

The magnitude and direction of a vector are both present. Dot product and cross product can be used to multiply two or more vectors. Let us learn more about each of the vector products.

There are two categories of vector products. The dot product of two vectors and the cross product of two vectors are based on the fact that a vector has both magnitude and direction. The dot product of two vectors is also known as the scalar product since the resultant value is a scalar quantity. Because the output is a vector that is perpendicular to these two vectors, the cross product is termed the vector product.

Dot product: The dot product of vectors is also known as the scalar product of vectors. The dot product of the vectors produces a scalar value. The dot product of vectors is the product of the magnitudes of two vectors and the cosine of the angle between the two vectors. When two vectors are dot producted, the resulting is in the same plane as the two vectors.

Cross Product: A Cross Product is also known as a Vector Product. The cross product is a sort of vector multiplication that involves multiplying two vectors of different types or natures. When two vectors are multiplied with each other and the product is likewise a vector quantity, the resultant vector is called the cross product of two vectors or the vector product.

How to find the magnitude of the vector product

The distance between the initial point P and the end point Q is the magnitude of a vector PQ. The magnitude of PQ ⃑is denoted as |PQ|⃑ in symbols.

The Distance Formula can be used to find the magnitude of a vector if the initial point and end point coordinates are known.

PQ⃑=(x2-x1)2+ (y2-y1)2

Example of find the magnitude of the vector product

Example: Determine the magnitude of the vector PQ ⃑, whose starting point is (1,1) and ending point is (5,3).

Solution: Use the Distance Formula to calculate your distance.

Substitute x1,y1.x2,y2

Answer: Magnitude of PQ is 4.5

Calculate vector product of 2 vectors

The cross product of two vectors is also known as the vector product.

The vector product of a and b is c if you have two vectors a and b.

c=a×b

As a result, the magnitude of c = ab sin , where is the angle between  a × b  and the direction of c is perpendicular to both a and b. What should this cross product’s direction be now? So we utilise a rule known as the “right-hand thumb rule” to determine the direction.

Curl our fingers from a × b to discover the direction of a to b. So, if we curl our fingers in the direction depicted in the diagram, your thumb will point upward in the direction of c. The direction of the cross product is shown by this thumb.

When applying rules to direction, smaller angles should be rotated, such as angle 180° between a and b. As a result, the fingers should be curled in an acute angle between a and b at all times.

Example: Determine the angle formed by 2i + 3j + k and 5i -2j + 3k.

Solution: The two vectors are as follows

As a result, the angle between the vectors is 72.3°.

Conclusion

We study, the vector product is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space indicated by the symbol.

Vectors are mathematical elements that indicate both the direction and magnitude of an item. Because vectors are commonly depicted as a line segment with an endpoint on one side and an arrow on the other, they are drawn to seem like rays.