Watch Free Classes

Parallel lines are defined as two or more lines that reside in the same plane but never intersect. They are exactly the same distance apart and have the same slope. 

Parallel lines in geometry are the lines which do not cross at any point or intersect each other. Curves that do not touch or intersect and maintain a predetermined minimum distance are known as parallel curves. A line and a plane that does not share a point in three-dimensional Euclidean space are also said to be parallel. Skew lines, on the other hand, are two non-coplanar lines.

Euclid’s parallel postulate deals with parallel lines. Parallelism is largely a feature of affine geometries, of which Euclidean geometry is a specific example. Lines can have equivalent features in other geometries, such as hyperbolic geometry, which is referred to as parallelism.

Parallel Lines and Transversal

Many pairs of angles are created when any two parallel lines are intersected by a transversal. Some angles are complementary, whereas others are congruent (equal). Look at the parallel lines labelled l and m that are cut by a transversal line n in the diagram below. The two parallel lines and a transversal have created eight different angles. An alphabet has been used to mark each angle.

l1

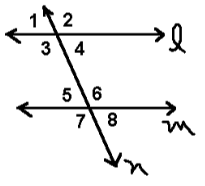
The angles created by the two parallel lines l and m are listed below.

  • Corresponding Angles: It’s worth noting that the corresponding angles are of identical magnitude. There are four pairs of corresponding angles in the above figure: ∠1 = ∠5, ∠2 = ∠6, ∠3 = ∠7, and ∠4 = ∠8.
  • Alternate Interior Angles: On the inside of two parallel lines intersected by a transversal, alternate interior angles are generated. They are of equal size. ∠3 = ∠6, ∠4 = ∠5 in this diagram. 
  • Alternate Exterior Angles: On either side of the transversal, alternate exterior angles are generated in equal quantity. In this ∠1 = ∠8 and ∠2 = ∠7.
  • Consecutive Interior Angles, also known as co-interior angles, are supplementary angles created on the inside of the transversal. ∠3 + ∠5 = 180°, and ∠4 + ∠6 = 180° in this case.
  • Vertically Opposite Angles: When two straight lines connect and are of equal length, vertically opposite angles are generated. In this case, ∠1 = ∠4, ∠2 = ∠3, ∠5 = ∠8, and ∠6 = ∠7.

Parallel Line Properties

The basic qualities listed below can help you identify parallel lines.

  • Straight lines that are always the same distance apart are known as parallel lines.
  • No matter how far parallel lines are extended in any direction, they never intersect.

Apart from the qualities listed above, the following properties can be used to identify any two parallel lines that are cut by a transversal.

  • If the angles formed by any two lines are equal, they are said to be parallel.
  • If the Alternate interior angles formed by two lines are equal, they are said to be parallel.
  • If the Alternate Exterior Angles formed by two lines are equal, they are said to be parallel.
  • If the interior angles on the same side of the transversal are additional, two lines are said to be parallel.

Parallel Lines Equation

A straight line’s equation is usually stated in the slope-intercept form, which is represented by the equation y = mx + b, where ‘m’ is the slope and ‘b’ is the y-intercept. The slope or gradient is determined by the value of ‘m,’ which informs us how steep the line is.

It’s worth noting that the slope of any two parallel lines is the same. If the slope of a line with the equation y = 4x + 3 is 4, for example. As a result, any line parallel to y = 4x + 3 has the same slope, which is 4. Parallel lines share no points and have different y-intercepts.

Conclusion

Parallel lines are two lines in the same plane that are at the same distance from each other but never meet in geometry. Parallel lines are defined as two or more lines that reside in the same plane but never intersect. They are exactly the same distance apart and have the same slope. Parallel lines in geometry are the lines which do not cross at any point or intersect each other.

A line and a plane that does not share a point in three-dimensional Euclidean space are also said to be parallel. Skew lines, on the other hand, are two non-coplanar lines.

Many pairs of angles are created when any two parallel lines are intersected by a transversal. Some angles are complementary, whereas others are congruent (equal). 

Straight lines that are always the same distance apart are known as parallel lines.

No matter how far parallel lines are extended in any direction, they never intersect.

A straight line’s equation is usually stated in the slope-intercept form, which is represented by the equation y = mx + b, where ‘m’ is the slope and ‘b’ is the y-intercept.