Profile
Settings
Refer your friends
Sign out
The curves formed by the intersection of a plane with a cone are known as conic sections or cone sections. A cone or conic section has three principal sections: parabola, hyperbola, and ellipse (the circle is a special kind of ellipse). The conic portions are made using a cone with two identical nappes.
Although the shapes of the sections of a cone or conic sections vary, they all share some common qualities, which we shall discuss in the following sections. Let’s look at the formulas for conic sections, conic equations, and their parameters, along with examples and FAQs.
Conic Section
Conic sections are the curves created by cutting a cone with a plane. Nappes are two similar conical shapes that make up a cone. Depending on the angle of the cut between the plane and the cone and its nappe, we can get a variety of shapes. We generate the following shapes by cutting a cone with a plane at various angles:
- Circle
- Parabola
- Ellipse
- Hyperbola
Ellipse is a conic section generated when a plane intersects a cone at a right angle. The circle is a sort of ellipse in which the cutting plane is parallel to the cone’s base. When the fascinating plane is parallel to the axis of the cone and intersects both nappes of the double cone, a hyperbola is created. We get a parabola conic section when the intersecting plane cuts at an angle to the surface of the cone.
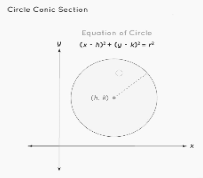
Conic Section of a Circle
The circle is a sort of ellipse in which the cutting plane is parallel to the cone’s base. The circle’s focus is known as the circle’s centre. The radius of the circle is the distance between the locus of the points on the circle and the focus or centre of the circle. For a circle, the value of eccentricity(e) is e = 0. There is no directrix in Circle. The general version of the equation for a circle with a radius of r and a centre at (h, k):
(x−h)² + (y−k)² = r²
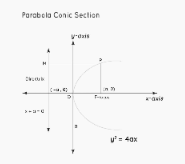
Conic Section of a Parabola
A parabola is a conic section formed when the intersecting plane is at an angle to the cone’s surface. It’s a conic section with a U shape. The eccentricity(e) value for a parabola is e = 1. The intersection of a cone with a plane parallel to its side produces an asymmetrical open plane curve. A parabola is a line-symmetric curve that has the same shape as the graph of y = x². A parabola’s graph can either open upwards, as in y = x², or downwards, as in y = – x². Under the effect of gravity, a projectile’s journey should ideally follow a curve of this shape.
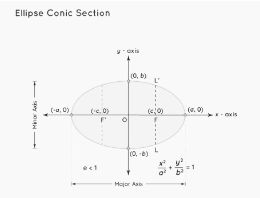
Conic Section Ellipse
Ellipse is a conic section generated when a plane intersects a cone at a right angle. Ellipse features two foci, as well as a major and minor axis. For an ellipse, the eccentricity(e) value is e<1. Ellipse has two axes of rotation. The general form of an elliptical equation with the centre at (h, k) and the major and minor axis lengths of ‘2a’ and ‘2b’, respectively. The ellipse’s primary axis is parallel to the x-axis. For an ellipse, the conic section formula is as follows.
(x−h)²/a² + (y−k)²/b² = 1
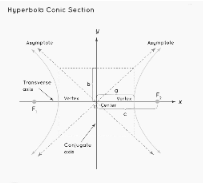
Conic Section Hyperbola
When the fascinating plane is parallel to the axis of the cone and intersects both nappes of the double cone, a hyperbola is created. For hyperbola, the eccentricity(e) value is e > 1. Branches are the two unconnected parts of the hyperbola. Their diagonally opposing arms approach the line’s boundary, and they are mirror reflections of each other.
A hyperbola is a conic section that can be constructed on a plane that crosses two nappes to form a double cone.
The following is the generic form of the hyperbola equation using (h, k) as the centre.
(x−h)²/a² – (y−k)²/b² = 1
Conclusion
Conic sections are the curves created by cutting a cone with a plane. Nappes are two similar conical shapes that make up a cone. Depending on the angle of the cut between the plane and the cone and its nappe, we can get a variety of shapes. The circle is a sort of ellipse in which the cutting plane is parallel to the cone’s base. The circle’s focus is known as the circle’s centre. The radius of the circle is the distance between the locus of the points on the circle and the focus or centre of the circle. A parabola is a conic section formed when the intersecting plane is at an angle to the cone’s surface. It’s a conic section with a U shape. The eccentricity(e) value for a parabola is e = 1. Ellipse is a conic section generated when a plane intersects a cone at a right angle. Ellipse features two foci, as well as a major and minor axis. For an ellipse, the eccentricity(e) value is e<1. When the fascinating plane is parallel to the axis of the cone and intersects both nappes of the double cone, a hyperbola is created. For hyperbola, the eccentricity(e) value is e > 1.
