Profile
Settings
Refer your friends
Sign out
The Binomial theorem provides a quick way to raise (or expand) a binomial statement to enormous powers. This is a crucial aspect of algebra. Permutations and combinations are discussed, as well as probability matrices, permutations, and mathematical induction. It’s an algebraic statement with two different terms connected by a + or – sign.
Humans have known about the binomial theorem since the fourth century BC. The binomial cubes came into usage during the 6th century AD and in the 10th century AD, an Indian mathematician named Halayudha used Pascal’s triangle to describe this procedure.
Index for Binomial Theorem
Binomial theorem for positive integral indices
According to the binomial theorem, the total number of terms in an expansion is always more than the index. Take, for example, an expansion of (a + b)n with n+1 terms and n as the index of the equation (a + b)n, where n is any positive integer.
The binomial theorem can be used to extend (x + y)n, where n is any rational number. Let’s look at the binomial theorem for positive integral indices.
The binomial theorem is a rule that can be used to enlarge any power of a binomial.
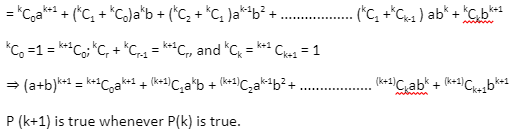
Therefore, P(n) is true for all positive integral values of n.
Properties of binomial theorem
- In the binomial expansion of (x+y)n, the number of coefficients is (n+1).
- In the expansion of (x+y)n, there are (n+1) terms.
- xn and yn are the first term and last term respectively.
- The powers of x decrease from n to 0 as the expansion advances, whereas the powers of y increase from 0 to n.
- The (r +1)th in the general term of of expansion is (x + y) n, which may be written as Tr+1=nCr xn-ryr.
- The coefficients of binomial expansion are organised into Pascal’s triangle.
- The nth term from the end of (x-y)n equals the (n-r+2)th term from the beginning in binomial expansion.
- The middle term in (x + y)n is (n/2)+1 if n is even; however, if n is odd, the middle terms are (n+1)/2 and (n+3)/2.
Coefficient of binomial theorem
The binomial coefficients are the figures associated with the variables x, y, in the expansion of (x +y)n. The binomial portions are represented as nC0, nC1, nC2. The binomial coefficients are attained through the Pascal triangle or by using the combinations formula.
Conclusion
The binomial expansion has more application than algebra II. In statistics, it is used to calculate the binomial distribution.
This allows statisticians to quantify the risk of a certain number of positive results in a set of trials.
Binomial expansion is also intriguing from a fine perspective as it allows mathematicians to gain insight into the properties of polynomials.
Binomial developments are used in numerous numerical and logical calculations, including kinematic and gravitational time enlargement, active energy, electric quadrupole post and determining the relativity factor gamma, to mention a few.
The number of terms in a binomial expansion of a binomial articulation raised to some power is another factor of the binomial development.
