Profile
Settings
Refer your friends
Sign out
The simplest type of number system is binary, which employs only two digits of 0 and 1. (i.e. value of base 2). Because digital electronics only has two states (either 0 or 1), current computer engineers, networking and communication specialists, and other professions favor binary numbers.
The decimal number system, on the other hand, is the most widely used number system. Base 10 is made up of only ten symbols: 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9.
Every number system has a base, which is determined by the total number of digits in the system. The binary number system, for example, has a base of two since any number is represented by only two digits. Similarly, the decimal number system has a base of ten since each number is represented by ten digits.
The binary to decimal conversion is significant because it allows you to read numbers that are represented as a series of 0s and 1s.
Binary to decimal conversion logic
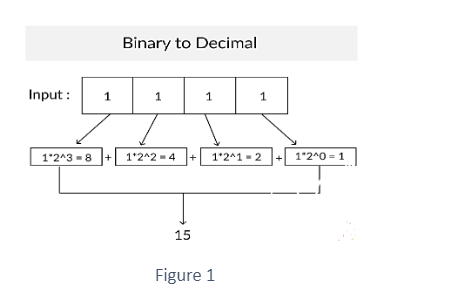
A program that converts a binary number to a decimal value. For instance, binary number 1111 has a decimal equivalent of 15.
Binary to Decimal Conversion Methods
The binary to decimal conversion is performed to make large binary values easier to interpret in a human-readable format. There are two ways to convert a binary number to a decimal value.
- Positional Notation Method
- Doubling Method
Positional Notation Method: The value of a digit in a number is defined by a weight based on its position in a number using the positional notation approach. This is accomplished by multiplying each digit by the base (2) increased to the appropriate power, which is determined by the digit’s location in the number. The total of all these values collected for each digit is the decimal equivalent of the provided binary number.
To understand the binary to decimal conversion, follow the steps below. Let’s use the binary number
(101101)2 as an example. The ‘Least Significant Bit’ (LSB) is the rightmost digit in any binary number, whereas the ‘Most Significant Bit’ is the leftmost digit (MSB). The least significant bit in a binary number with ‘n’ digits has a weight of 20 and the most significant bit has a weight of 2n-1.
Doubling Method: The method of doubling or multiplying by two is used to convert binary to decimal, as the name implies. The method of doubling or multiplying by two is used to convert binary to decimal, as the name implies. To convert the binary number (101101)2 to decimal, we’ll apply the same example.
(101101)2 as an example. The ‘Least Significant Bit’ (LSB) is the rightmost digit in any binary number, whereas the ‘Most Significant Bit’ is the leftmost digit (MSB). The least significant bit in a binary number with ‘n’ digits has a weight of 20 and the most significant bit has a weight of 2n-1.
Formula of Binary to Decimal Conversion
The formula to convert binary to decimal is provided as, where dn is the digits of a binary integer of ‘n‘ digits.
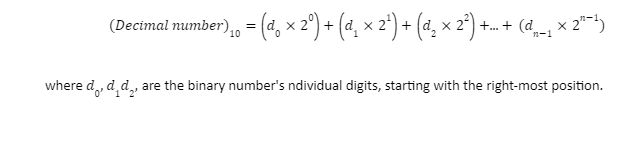
Binary to decimal converter circuit diagram
Binary to decimal converter to double-check the results of your manual calculations to convert a number supplied in binary to its decimal counterpart – Binary to Decimal Calculator
A 4-bit binary to decimal encoder’s logic diagram is shown here.
Example of Binary to Decimal Conversion
Let’s look at an example to better grasp the conversion. Let’s look at how to convert 11012 to a decimal number.
Starting from the LSB, 11012 = (1×23)+(1×22)+(0×21) + (1×20)
= (1× 8)+(1×4)+(0×2)+(1×1)
= 8+4+0+1
= 1310
Thus, the decimal representation of 1101 is 13.
Conclusion
We learned, Binary to decimal conversion refers to the process of converting a binary number to a decimal number and many strategies for converting binary to decimal in the preceding sections. Check out this binary to decimal converter to double-check the results of your manual calculations to convert a number supplied in binary to its decimal counterpart – Binary to Decimal Calculator
