Profile
Settings
Refer your friends
Sign out
The prefix ‘bi’ denotes ‘two’ in this context. It’s termed binary because it has a two-digit base and exclusively employs the numbers 0 and 1. In computer technology, binary number systems are the most widely utilized. In their programming languages, all computers utilize a binary number system, which uses only two symbols: 0 and 1.
Binary division works in a similar way to long division in the decimal system. The dividend is still divided by the divisor in the same way, with the only difference being that binary subtraction is used instead of decimal subtraction. It’s worth noting that binary division requires a solid understanding of binary subtraction. For more information, see the example below and the binary subtraction section.
Rules for Binary Division
All arithmetic operations, such as addition, subtraction, multiplication, and division, can be performed on binary numbers in the same manner they can be done on the decimal number system. The four types of arithmetic operations performed here are binary subtraction, binary multiplication, binary addition, and binary division. When dividing two binary numbers, we only need to follow a few guidelines. When conducting binary division, there are four guidelines to follow. Division by 0 has no meaning in Binary division, just as it does in the decimal system (or any other number system). The following are the binary division rules:
Dividend | Divisor | Result |
o | 1 | o |
1 | 1 | 1 |
Because binary numbers only have two digits, the four rules listed above are all possible conditions for dividing binary numbers.
How binary division is performed
The long division method, which is one of the most efficient and easiest ways to divide binary integers, can be used to solve binary division difficulties. In a binary division operation, these are the steps to take:
Step 1: Make a comparison between the divisor and the dividend. If the divisor is greater, set the quotient to 0 and then lower the second bit of the dividend. If the divisor is less than one, multiply it by one to get the subtrahend. The remainder is obtained by subtracting the subtrahend from the minuend.
Step 2 : Then, from the dividend portion, bring down the next number bit and repeat step 1.
Step 3: Repeat Steps 1–3 until the remaining is zero or the dividend is divided in half.
Example of binary division
B=0110102 and C= 01012 are two binary numbers. We wish to divide B by C in this case.
Given, dividend 0110102 , c= 01012
Step 1: Remove the zero in the most significant bit position from both the dividend and divisor because it has no effect on the number’s value. As a result, the dividend is 110102 and the divisor is 1012.
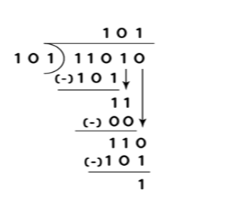
Step 2: Let’s apply the method of long division. Because the divisor is smaller than the first digit in the dividend 11010 2, it will be multiplied by 1 and the result will be the subtrahend.
The binary multiplication rules are as follows:
- 1 × 1 = 1
- 1 × 0 = 0
- 0 × 1 = 0
- 0 × 0 = 0
As a result, 101× 1 = 101 2 is the result, which is given below.
Step 3: Subtract the minuend 110 2 from the subtrahend 101 2.
According to the rules of binary subtraction,
We need to borrow 1 from the next more important bit because 0 – 1 = 1.
- 0 minus 0 equals 0
- 1 minus 1 equals 0
- 1 minus 0 equals 0
Step 4: Next, we write 0 as the quotient’s next bit, and then the least significant bit 0 descends.
Step 5: The divisor is multiplied by 1 once more, yielding 101 × 1 = 101 2. as the result.
Step 6: We’ve reached the end of the process. We subtract 1012 from 1102 using binary subtraction. 1102 – 1012 = 0012 is the result. Because all of the integers are the same, the remainder is comparable to Step 3.
Binary division logic
A divider circuit can be simply constructed using the binary division truth table. Consider the diagram below.
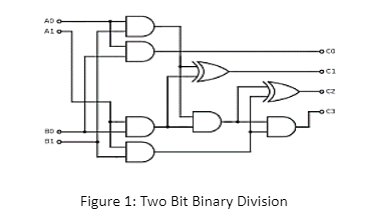
A two-bit divider circuit is depicted in the circuit diagram. A0, A1 for one number and B0, B1 for the other are the two bits input. The binary form representation of the quotient is represented by the pins C0, C1, C2, and C3. As indicated in the diagram, the circuit is built using AND gates and Ex-OR gates. Multiplexer and demultiplexer circuits are a popular application of logic gate operation.
Conclusion
We learn that the payout is divided by the divisor using only the digits 0 and 1 in binary division. The residual is the value left over after the division is complete, while the quotient is the outcome of the division. Binary division works in a similar way to long division in the decimal system. The dividend is still divided by the divisor in the same way, with the only difference being that binary subtraction is used instead of decimal subtraction.
