A curve’s asymptote is the point at which the curve converges. In other words, the curve and its asymptote approach each other infinitely but never meet. Asymptotes are useful for charting rational equations and are used in big O notation. They are also easy approximations to complex equations.
- Understanding the meanings of vertical, horizontal, and oblique asymptotes, as well as how to determine them algebraically.
- Understanding how to analyze limitations using various limit laws and attributes.
- Reviewing how asymptotes aid in the sketching of a function’s curve.
- Understanding the meanings of vertical, horizontal, and oblique asymptotes, as well as how to determine them algebraically.
- Understanding how to analyze limitations using various limit laws and attributes.
- Reviewing how asymptotes aid in the sketching of a function’s curve.
Asymptotes Types
There are 3 types of asymptote
- Horizontal asymptote – it is a horizontal line, it has the equation y = k.
- Vertical asymptote – it is a vertical line, its equation is in the form x = k.
- Oblique asymptote – it is a slanting line, it has the equation y = mx + b.
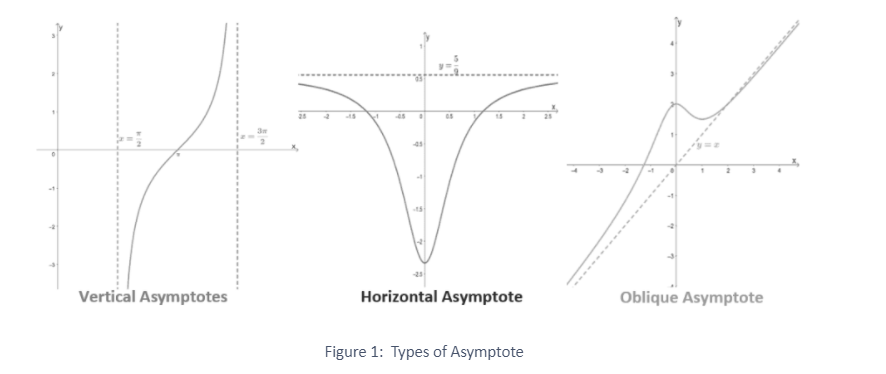
Asymptotes using equation
Vertical asymptotes can be obtained by solving the equation n(x) = 0, where n(x) is the function’s denominator this only applies if the numerator t(x) for the same x value is not zero). Find the function’s asymptotes. With the equation x = 1, the graph has a vertical asymptote.
Asymptotes exponential function
Certain functions, such as exponential functions, have a horizontal asymptote that is always present.
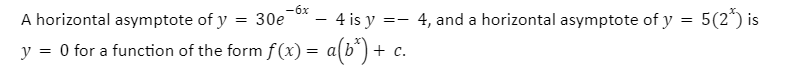
How to find asymptotes?
Identifying the types of asymptotes is simple when given the graph of a function that includes its asymptotes.
The equation for an asymptote is x = a, y = a, or y = ax + b because it is a horizontal, vertical, or slanting line. The rules for finding all forms of asymptotes of a function y = f(x). are as follows.
- A horizontal asymptote has the form y=k, where x→∞ or x→- is a positive or negative number. f(x) and f(x) .
- A vertical asymptote has the form x=k, where y→∞ or y– is a positive or negative number.
- The form of a slant asymptote is y = mx + b, where m is smaller than zero. It’s prevalent in rational functions, and mx + b is the quotient formed by dividing the rational function’s numerator by the denominator.
Example: The degree of the numerator in the function f(x) = (3×2 + 6x) / (x2 + x) is equal to the degree of the denominator (= 2). As a result, the horizontal asymptote is
Solution: y = (leading coefficient of numerator) / (leading coefficient of denominator)
=
3 ⁄ 1=3
As a result, it’s HA is y = 3.
Example:2 Find the domain of the following function, as well as all of its asymptotes:
y=x²+3x+1 ⁄ 4x²-9
4x²-9=0
4x²=9
x²=9 ⁄ 4
x=±3 ⁄ 2
The domain then becomes all x-values other than 3 ⁄ 2 The two vertical asymptotes are located at x=±3 ⁄ 2
Conclusion
In this article, we study about Asymptotes, their types, equations, and examples. Asymptotes are useful for graphing rational equations, according to this article. They are used in big O notation, are simple approximations to complex equations, and are used in big O notation. The asymptotes of a function are a crucial step in drawing its graph because they communicate information about the behavior of curves in the large. Asymptotes of functions, in a wide sense, are studied as part of the subject of asymptotic analysis.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






