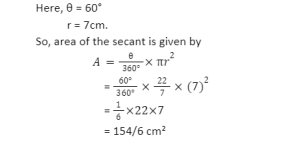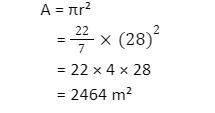From the viewpoint of the beginning of higher education, the areas related to the circle chapter is one of the most significant topics for Class 10 students. Few topics are designed in higher classes based on the features and applications of circles. So, let’s have a look at some of the key elements in this chapter’s discussion of circles:

• Basically a circle is the collection of all the points separated by a specified distance (radius) from a fixed point (center).
• A line and a circle in the same plane will not intersect. The line may come dangerously close to striking the circle at some point. The tangent to the circle is a line that is parallel to the circle. Because the line meets the circle at two locations, it is the secant for the circle.

Tangent to a circle:-

The line that meets the circle at a single point is called a tangent to the circle. The intersection of a tangent and a circle is known as the point of tangency. The tangent intersects the circle’s radius and is perpendicular to it. Tangents can be found in any curved shape. Tangent has its own equation because it is a line.

• The tangent will only come into contact with the circle once.
• The line containing the radius across a point of contact is referred to as ‘normal’ to the circle at the point.

Condition of Tangency:-

Only if a tangent hits a curve at a single place is it called a tangent. If not, it is simply referred to as a line. So, depending on where the point of tangency is in relation to a circle, we can specify the tangent criteria as follows:

• When the point is located within the circle.
• When the point is at the center of the circle.
• When a point is located outside of a circle.

Circumference of Circle:-

The circumference, often known as the perimeter, of a circle is the measurement of the circle’s boundaries. A circle’s area, on the other hand, determines the area it covers. When we open a circle and draw a straight line through it, the circumference is its length. It’s usually measured in centimeters or meters.

The circumference of a given circle, whose radius is r , is given as;

                    C = 2πr

Area of Circle:-

The region occupied by a circle in a 2D plane is referred to as its area. Using the formula A = πr², it can be determined. This formula can be used to calculate the area occupied by a circular field or plot. (R is the radius of a circle.)

Perimeter of the Semi-circle:-

A semicircle’s perimeter is equal to the sum of half of a circle’s circumference and its diameter. The perimeter of a circle is 2r or d, as we know. As a result, a semicircle’s perimeter will be πr + 2r or πr + d, where r is the radius and d is the diameter.

Sector of a circle:-

A sector is a segment of a circle that is between its two radii and the arc to the right. The most common sector of the circle is a semi-circle, which represents half of a circle. A circle with a sector can be broken further into two regions: the Major Sector and the Minor Sector. 

The length of the sector can be determined by using the following formula: