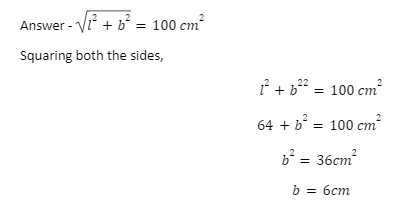Area Perimeter Formula

Area and perimeter are the most important aspects of 2D mensuration. We use it in many applications in our daily life. Areas is the space that is covered by a flat shape and perimeter is the boundary of any shape. We find area when we have to calculate the inside region of anybody and we find perimeter when we want to know the length of the boundary of a body. 

Throughout our mathematics studies, we have taught that the perimeter of a flat, two-dimensional object is the distance around it, and the area of a flat, two-dimensional shape is the amount of space taken up by the shape. In simple terms, the perimeter, or circumference, of a shape or thing is the distance or length around the shape or object and the area of the thing is the quantity of space it contains.

Area 

The total amount of space occupied by any two-dimensional figure is referred to as its area. To put it another way, it is the amount that counts the number of unit squares that cover the surface of a closed figure’s surface area. 

In geometry, the area of a flat shape or the surface of an item can be described as the space occupied by the shape or surface of the object.

The surface area of a closed figure is equal to the number of unit squares that cover the surface of the figure when it is closed. The area is measured in square units, such as square centimeters, square feet, square inches, and so on. 

Use of area in our daily life 

Every day, how is area used?

In what real-life situations do we need to use area? Floor covering, like carpets and tiles, need to be measured to make sure they fit. Wallpaper and paint also need to know how big the space is. Fabric that is used to make clothes and other things also needs to be thought about in terms of length and width.

Perimeter 

The perimeter of a shape is the distance that goes around the shape. How long is an outline or boundary of a 2-D shape? The perimeter of different shapes can be the same size, depending on the dimensions of the shapes that they are.

Use of perimeter in our daily life-

There are a lot of different ways perimeter is used in everyday life.

Many times, we find the perimeter when we put up Christmas lights around the house or fence the back yard garden. Some other examples might be finding the total length of the boundary of the soccer field or the length of the crochet or ribbon that is needed to cover the border of a table mat with crochet or ribbon.

Some important formulas

Rectangle 

Let us consider the length = l units and breadth = b units. 

1. Area of the rectangle = (l*b) units.

2. Length = (area / breadth) units.

3. Breadth = (area/length) units.

4. Diagonal = √l2+b2 units.

5. Peremeter = √2l+bunits.

Area of 4 walls of a room.

Let us consider a room of length = l units and breadth = b units and height = h units. 

1. Area of 4 walls = 2l+b*hsq units.

2. Diagonal of the room = √l2+b2+h2 units.

Square 

Let us consider a square each of whose sides = a.

1. Area of a square = a2 sq units 

2. Side of a square = (area ) units.

3. Diagonal of a square = (2 a )units.

4. Area of the square = [12 X(diagonal)2]sq units

5. Perimeter of the square = (4a) units. 

Circle  

Let r be the radius of circle 

1. Area of a circle=πr2

2. π = 22/7 

perimeter in case of a circle is known as the circumference of a circle, which is equals to 2πr

3. C = 2πr where r is the radius of the circle.

Triangle 

1. Area of a triangle =1/2 base x height

2. Area of equilateral triangle = √3/4 x a2

Rhombus 

In case of rhombus all sides are equal and diagonals bisect each other at 90°

1. Area of a rhombus = ½ x length of 1st diagonal x length of 2nd diagonal. 

Trapezium 

In trapezium one pair of opposite side is parallel and the one is non- parallel 

Area of trapezium =  ½ x (a+b) x h 

Heron’s formula

Area= √ S(S-a)(S-b)(S-e)

Where a,b,c are lengths.

S= a+b+c / 2 

Parallelogram 

In this opposite sides are parallel and equal.

Area of parallelogram = base x height 

Conclusion 

Area and perimeter are the most important aspects of 2D mensuration. Areas is the space that is covered by a flat shape and perimeter is the boundary of any shape. In geometry, the surface of an item can be described as the space occupied by the shape or surface of the object. In geometry, the area of a flat shape or the surface of an item can be described as the space occupied by the shape or surface of the object.

 The surface area of a closed figure is equal to the number of unit squares that cover the surface of the figure when it is closed. Area is measured in square units, such as square centimeters, square feet, square inches, and so on. The perimeter of a shape is the distance that goes around the shape- how long is an outline or boundary of a 2-D shape?