Profile
Settings
Refer your friends
Sign out
Similar figures are geometric forms that have the same shape but differ in size. If the respective angles are equal and the corresponding sides are proportionate, two triangles are said to be similar. The two requirements in the above definition are mutually exclusive. If one of the two conditions is true, the other is true as well. As a result, comparable triangles can be defined using either of the two conditions. Not only do similar triangles have similar angles and sides, but also their perimeters, areas, and other characteristics are proportional.
Although the two comparable triangles have the same shape, their sizes may differ. Similar triangles have the same ratio of matching sides. Each pair of comparable triangles’ matching angles is the same.
SIMILAR TRIANGLE:-
If two triangles have the same ratio of corresponding sides and an equal pair of corresponding angles, they are comparable. When two or more figures have the same shape but differ in size, they are referred to as comparable figures.
If two triangles are similar, they are said to be comparable.
- Their respective angles are the same
- The proportions of the corresponding sides are proportionate.
If we have the two triangle ∆ABC and ∆ PQR
Then ∠A = ∠P , ∠B = ∠Q and ∠C = ∠R
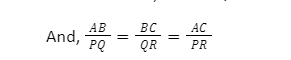
Not only do similar triangles have similar angles and sides, but they also have similar perimeters, altitudes, angle bisectors, areas, and other characteristics.
AREA OF SIMILAR TRIANGLE:-
Area of triangles that are comparable Theorems can help you figure out how the areas of two comparable triangles are related. “The square of the ratio of any pair of their corresponding sides is equal to the ratio of the areas of two identical triangles,” it says. Take a look at the diagram below, which depicts two comparable triangles, ∆ABC and ∆DEF
PROOF OF AREA OF SIMILAR TRIANGLE:-
Statement:- The square of the ratio of any pair of their respective sides is equal to the ratio of the areas of two identical triangles.
Given: Consider the following two triangles: ∆ABC and ∆DEF. And ∆ABC ~ ∆DEF.
To prove:- Area of ABC/Area of DEF = (AB)²/(DE)² = (BC)²/(EF)²= (AC)²/(DF)² .
Construction:- To the sides BC and EF, draw the perpendicular AP and DQ, respectively.
Proof:- Since ∠B = ∠E ……..(ΔABC ~ ΔDEF)
and, ∠APB = ∠DQE…..[AP and DQ are perpendicular on sides BC and EF, respectively, and both angles are 90 degrees]
We can see that ABP and DEQ are equiangular using the AA property of triangle similarity.
As a result, ΔABP ~ ΔDEQ .As a result, AP/DQ = AB/DE. This also suggests that:BC/EF = AP/DQ ——- (1)
Thus, Area(ΔABC)/Area(ΔDEF) = [(1/2) × BC × AP]/[(1/2) × EF × DQ]
= (BC/EF) × (AP/DQ)
= (BC/EF) × (BC/EF) ….[from (1)]
⇒ Area(ΔABC)/Area(ΔDEF) = (BC/EF)²
In the similar manner, we may demonstrate that,
Area of ΔABC/Area of ΔDEF = (AB)²/(DE)² = (BC)²/(EF)² = (AC)²/(DF)²
Hence proved.
POINTS TO KEPT IN MIND:-
- The square of the ratio of any pair of their respective sides is equal to the ratio of the areas of two identical triangles.
- Area of ABC/Area of DEF = (AB)2/(DE)2 = (BC)2/(EF)2 = (AC)2/(EF)2
- For identical triangles, all corresponding angle pairs are equal, and all corresponding sides are proportional.
- The ratio of the squares of the matching medians determines the area of two identical triangles.
- The ratio of the squares of corresponding elevations is the area of two similar triangles.
- The ratio of the squares of the respective angle bisector segments determines the areas of two identical triangles.
- When the areas of two identical triangles are equal, the triangles are congruent, meaning they are equal and similar.
CONCLUSION:-
The square of the ratio of any pair of comparable triangles’ corresponding sides is equal to the ratio of the area of two similar triangles. When two triangles are comparable, their respective angle pairs are equal and their corresponding sides are proportional.
Geometric figures with the same shape but various sizes are known as similar figures. Two triangles are considered to be similar if their respective angles are equal and their corresponding sides are proportionate.
