The Pentagon belongs to the Polygon family of Geometric Shapes. The word “Pentagon” derives its origins from the Greek Word “Pentagonos”. The word “Pentagonos” means five-angled”. The pentagon can be defined as a two-dimensional closed geometric shape with five vertices connected by five sides. Now we will look at the figures of both The regular pentagon and the irregular pentagon to help us understand the difference between them better.
Regular Pentagon vs. Irregular Pentagon-
Now we will see figures pertaining to both The Regular Pentagon and The Irregular Pentagon to help us better understand the topic.
In a Regular pentagon, all external angles are equal to each other and all internal angles are equal to each other. The measures of the Internal Angles are equal to 108° and the measures of the External Angles are equal to 72°. All the sides of The Regular Pentagon are equal in measure to each other. The sides of The Regular Pentagon are all straight. The sum of the Interior Angles in The Regular Pentagon is equal to 540°.
Now we will look at an Irregular Pentagon.
The above figure depicts an Irregular Pentagon. This figure shows three Irregular Pentagons. Now we will see some properties of The Irregular Pentagon. In The Irregular pentagon, all the angles may be of different measures and the sides of The Irregular Pentagon may be of different sides.
Now we will see the two very common types of Irregular Pentagons:- The Concave Pentagon and the Convex Pentagon. Now we will look at some of the properties of The Convex Pentagon and the concave Pentagon.
In a Convex Pentagon, all the interior angles are less than 180°. Also, in a Convex Pentagon all the corners are bent out of shape. A particular Convex Pentagon can be either a Regular Pentagon or an Irregular Pentagon.
The Perimeter of a Pentagon-
The Perimeter of a particular Geometric Shape or Figure is the length of its boundary.
Now we will move on to the Physical Dimensions of The Pentagon. We will start here with the Perimeter of The Pentagon.
There are different methods to calculate The Perimeters of The Regular Pentagons and The Irregular Pentagons.
For the Regular Pentagon, if we assume that the length of a side is a,
Perimeter (P) is given by,
P=5*a
P=5a
Now for the Irregular Pentagon, if the lengths of the sides are a, b, c, d, e
The Perimeter (P) is given by,
P=a+b+c+d+e
We have considered 5 different side lengths because the sides of an Irregular Pentagon might be all different in length.
Area-
The area of a Particular Geometric Shape is the Area inside the boundary of that particular Geometric Shape.
In this case, The Area of a Pentagon is the area of the space enclosed by The Pentagon.
Now we move on to the most important topic in this chapter, which is how to find out the Area of a Pentagon. Finding the Area of a Pentagon is a much more complicated process than finding out The Perimeter.
So, to find out The Area of a Regular Pentagon, The Regular Pentagon must be divided into five triangles. This step can be done by drawing five lines from the centre of the Pentagon.
So now that we have the triangles, we have to find out the Area of one of those triangles. We can find the area of the triangle by any of the two methods.
A= (1/2)*b*h
Where,
b: length of the base of the triangle.
h: length of the height of the triangle.
A=√s(s-a)(s-b)(s-c)
Where,
s= semi-perimeter of the triangle.
s= (a+b+c)/2
a: length of the first side of the triangle.
b: length of the second side of the triangle.
c: length of the third side of the triangle.
So, now that we have calculated the area of the triangle, we will multiply it by five to find out The Total Area of The Regular Pentagon. This is because the regular pentagon has five triangles.
If we have to find out the Area of an Irregular Pentagon, we can draw an appropriate number of triangles, find out the area of those triangles and add up those areas, we can find out The Total Area of the Irregular Polygon.
Now we will solve some problems related to the topics discussed above.
Examples-
- Find the perimeter of a Regular Pentagon with a side equal to 5.
Soln.
Given:
a=5
P=5a
P=5*5
P=25
So the Perimeter of The Regular Pentagon is 25.
- Find the perimeter of a Regular Pentagon with a side equal to 7.
Soln.
Given:
a=7
P=5a
P=5*7
P=35
So the perimeter of The Regular Pentagon is 35.
- Find the Perimeter of an Irregular Pentagon with sides equal to 3, 5, 7, 9 and 11.
Soln.
The perimeter of an Irregular Pentagon is the sum of the measures of its sides.
P=3+5+7+9+11=35
Conclusion
In this chapter, first, we have defined the pentagon. Then we moved on to the Introduction. In the Introduction topic, we saw The Pentagon in detail. Then we saw the difference between The Regular Pentagon and The Irregular Pentagon using images. Then we saw how to calculate the perimeters of both the regular pentagon and the irregular pentagon. After that, we saw how to calculate the area of The Regular Pentagon and The Irregular Pentagon. Then we solved some problems related to these topics.
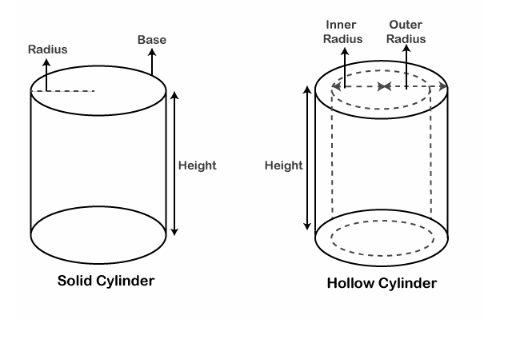
In this figure, we can easily see the difference between a Solid Cylinder and a Hollow Cylinder. We can briefly describe the difference between The Hollow Cylinder and The Solid Cylinder as, The Solid Cylinder is Solid in shape, meaning, it has no empty space between its boundaries, whereas The Hollow Cylinder has empty space between its boundaries.
We can also see from the above figure that The Solid Cylinder has only one Radius mentioned in the above figure. In the Hollow Cylinder, there are two radii, mentioned as “Internal Radius” and “External Radius”. We will further see the difference between The Hollow Cylinder and The Solid Cylinder when we try to calculate The Area and The Volume of both The Hollow Cylinder and The Solid Cylinder.
Area
In this topic, we will see the Area of both The Hollow Cylinder and The Solid Cylinder.
First, we will see how to calculate the Area of The Hollow Cylinder.
To calculate the Total Surface Area (TSA) of a Hollow Cylinder, we have to calculate the Lateral Surface Area (LSA) first.
So,
Lateral Surface Area is equal to the sum of External Surface Area (ESA) and Internal Surface Area (ISA).
So, to calculate that,
LSA=ESA+ISA
LSA=2*π*R*h+2*π*r*h
LSA=2πRh+2πrh
LSA=2πh(R+r)
This is Lateral Surface Area.
Now, The Total Surface Area (TSA) is the sum of The Lateral Surface Area (LSA) and the Sum of The Areas of The Solid Bases (ASB).
TSA= LSA+ASB
TSA= 2πh(R+r) + 2π (R2r2)
Now we will calculate the Area of the Solid Cylinder and below we will see a figure to help us understand this.

Now we will calculate the Total Surface Area (TSA) of this Solid Cylinder. But first, we have to calculate the Curved Surface Area (CSA).
CSA=2*π*r*h
CSA=2πrh
So the Total Surface Area (TSA),
TSA= 2πrh + πr2+πr2
TSA= 2πrh + 2πr2
TSA= 2πr (h+r)
Volume
Now we will have to calculate the volumes of both The Hollow Cylinder and The Solid Cylinder. In order to do that, we have to see the figures pertaining to both The Hollow Cylinder and The Solid Cylinder.
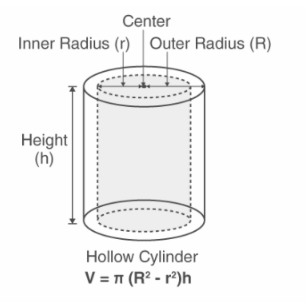
From the above figure, we can see that the Volume of The Hollow Cylinder is equal to,
V=π (R2 -r2)h
Now we will see how to calculate the Volume of a Solid Cylinder with the help of a diagram:-

The volume of the Solid Cylinder like the one given in the above figure is:-
V=πr2h
So now that we have calculated the Area and Volume of both The Hollow Cylinder and The Solid Cylinder, we can now move to some solved problems that will use the topics that we have just learned.
Solved Problems
- Find the volume of a Hollow Cylinder whose outer radius is 9 and whose internal radius is 7 and whose height is 9. (Use π= (22/7)).
Soln.
As we have learned earlier in this topic, Volume of a Hollow Cylinder,
V=π (R2-r2) h
V= (22/7) *(92-72)*(9)
V= (22/7) *(81-49)*(9)
V= (22/7)*288
V=905.143
- Find the volume of a Hollow Cylinder whose Outer Radius is 12 and whose internal radius is 8 and whose height is 7. (Use π= (22/7)).
Soln.
As we have learned earlier in this topic, Volume of a Hollow Cylinder,
V=π (R2-r2) h
So substituting the values given in the question in the above formula,
V= (22/7) *(122-82)*(7)
V= (22/7) *(144-64)*(7)
V=1760
- Find the volume of a solid cylinder with radius=5 and height=5. (Use π= (22/7)).
Soln.
As we have learned in the above topics,
V=πr2h
V= (22/7)*(52)*(5)
V= (22/7)*(53)
V=392.857
- Find the volume of a solid cylinder with radius=7 and height=6. (Use π=(22/7)).
Soln.
As we have learned in the above topics, the volume of a Solid Cylinder is given by:-
V=πr2h
V= (22/7)*(72)*(6)
V=924
- Find the area of a hollow cylinder with an external radius 7, an internal radius of 6, and a height of 5. (Use π= (22/7)).
Soln.
We already know the formula of Area of a Hollow Cylinder,
TSA= 2πh(R+r) + 2π (R2-r2)
TSA= 2× (22/7) × 5× (7+6) + 2× (22/7) × (72-62)
TSA=2× (22/7) × 5 × 13 + 2× (22/7) ×13
TSA= 408.571+81.714
TSA=490.285
- Find the area of a hollow cylinder with an external radius 9, an internal radius of 6, and a height of 4. (Use π= (22/7)).
Soln.
We already know the formula of Area of a Hollow Cylinder,
TSA= 2πh(R+r) + 2π (R2-r2)
TSA= 2× (22/7) ×4× (9+6) + 2× (22/7) × (92-62)
TSA=377.143+282.857
TSA=660
- Find the area of a solid cylinder with a radius of 5 and height of 3. (Use π= (22/7)).
Soln.
Area of a solid cylinder,
TSA= 2πr (h+r)
TSA= 2× (22/7) ×5× (3+5)
TSA= 251.428
- Find the area of a solid cylinder with a radius of 6 and height of 4. (Use π= (22/7)).
Soln.
Area of a solid cylinder,
TSA= 2πr (h+r)
TSA= 2× (22/7) × 6 × (4+6)
TSA= 377.143
Conclusion
In this article, we described The Hollow Cylinder in brief. Then we compared the Hollow Cylinder with the Solid Cylinder. We discussed how to calculate the hollow cylinder and The Solid Cylinder. We talked about how to calculate the volume of both of these geometric figures. Finally, we solved some problems related to these topics.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






