The Binomial Theorem is the formula for expanding any binomial statement’s power into a series. A Binomial Theorem can help you solve binomial expressions fast. It presents an expression to calculate the expansion of (a+b)n for every positive integer n. A binomial expression, such as 4x2+9, is a two-term algebraic statement. However, finding a solution becomes complex when statements have an enormous power or index. As a result, the Binomial Theorem was established, allowing you to multiply or expand a binomial expression quickly.
Applications of Binomial Theorem
1. Finding e (Euler’s Number)
As we know, e = 2.71828182846
Here, e =(1 + 1/n)n
 By calculating, we get:
By calculating, we get:
e= 2.7083
2. Divisibility and remainder problem
For example- If we divide 3230 by 7, what will be the remainder?
We know, 25 = 32,
3230 can be written as:
(25)30 = 2150 = (23)50 = 850 = (7 + 1)50
= [ (7)50 + 50C1(7)49 + 50C2 (7)48 + … + 1]
= [7 ( (7)49 + 50C1(7)48 + 50C2 (7)47 + … ) + 1 ]
Now, (7k + 1)/7, gives us the remainder 1
3. Finding the greatest term
- If n>6, then nn< n3n <3n!
- n ≥ 1 and n ∈ N, 2 ≤ (1+1/n) < 3
This theorem can be used in solving problems such as which one is greatest among 100100 and (300!)
From the result
Insert n= 300
= (100)300 < (300)! ………(i)
But, (100)300 > (100)100 ………(ii)
From equation (i) and (ii)
= (100)100 < (100)300 < (300)!
Therefore, (100)100 < (300)!
Binomial Theorem Expansion
The binomial expression is particularly significant in binomial theorem expansion in an algebraic equation with two separate terms.
For any positive integer n, it gives an expression to calculate the expansion of (a+b)n. The Binomial Theorem is defined as follows:
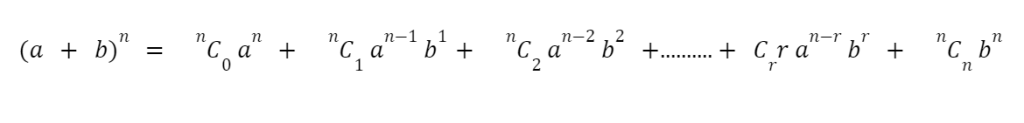
Real-life Use of Binomial Theorem
Economy
The impact of the economy may be calculated using the binomial mathematical theorem. The US economy, which runs a substantial part of the economy on probabilistic analysis, is a real-life illustration of this. The binomial theorem can forecast how a country’s economy will perform in the near future. It has a lot of importance in terms of making accurate economic forecasts.
Higher Mathematics
The binomial theorem is a mathematical formula used to perform complicated and virtually impossible calculations. Binomial theorems were used extensively in several of Sir Albert Einstein’s equations, laws, and theories. Therefore, this theorem’s notions are extremely valuable in research, mathematical analysis, or project.
Forecast services
It has the potential to be used in weather prediction services. It is essential for forecasting and understanding weather trends. We can use the existing data to forecast the weather for the next few days or weeks. This has a significant impact on our lives. The binomial theorem can also be used to forecast impending disasters. This has the potential to save lives: We can save many people’s lives by predicting disasters like tsunamis and cyclones.
Probability
Probability is one of the key fields in which this theorem is essential. For example, binomial probability is a notion that assists us in determining the likelihood of x successes in n repeated trials with two alternative outcomes, such as the probability of getting tails seven times while tossing a coin 15 times.
Conclusion
Because of its simplicity and understandability, the binomial theorem may be applied in various situations, such as generating economic predictions or weather forecasting. You might be using it in your daily life without realizing it. A Binomial Theorem is a simple approach to expanding a binomial statement with big powers. This theorem has applications in Permutations and Combinations, Probability, Matrices, and Mathematical Induction and is a vital topic (part) in algebra.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






