Introduction: Trigonometry is a discipline of mathematics that studies the relationship between the ratios of a right-angled triangle’s sides and its angles. The concept of trigonometry was introduced by the Greek mathematician Hipparchus, while the name trigonometry is a 16th century Latin derivative.
One of the most significant branches of mathematics is trigonometry. The terms ‘Trigonon’ and ‘Metron,’ which imply triangle and measure respectively, are combined to form the word trigonometry.. It thus facilitates the use of formulas and identities based on this relationship to find the measure of unknown dimensions of a right-angled triangle.
- Basics of Trigonometry
The measurement of angles and problems involving angles are covered in the fundamentals of trigonometry. Other essential trigonometric functions can be derived using these three basic ratios or functions: cotangent, secant, and cosecant. These functions form the foundation for all of the fundamental topics in trigonometry. As a result, in order to comprehend trigonometry, we must first study these functions and their formulas.
The three sides of a right triangle are as follows.
The side that is opposite to the angle θ is called perpendicular.
The angle θ neighboring side is called the base.
The hypotenuse is the side that is opposite the right angle.
- Trigonometry in Real-Life Situations
Many real-life applications of trigonometry can be found. Let’s use an example to help us understand trigonometry. Near a tree, a young boy stands. “How tall is the tree?” he inquires as he glances up at it. Without actually measuring the tree, the height can be determined. A right-angled triangle is one in which one angle out of three is 90 degrees. If the distance between the tree and the boy, as well as the angle formed when the tree is observed from the ground, trigonometric formulas can be used to compute the height of the tree.
It is calculated using the tangent function, for example, tan of angle is the ratio of the tree’s height to the distance. Let’s imagine the angle is, and we’ll state
tanθ = Height/Distance between item and tree
Distance = Height/tan θ
- What Do You Mean When You Talk About Height and Distances?
The following are the most important definitions used when dealing with heights and distances:
- Line of Sight– The line drawn from an observer’s eye to a point in the object viewed by the observer is known as the line of sight.
- The angle of Elevation: The elevation angle is the angle formed between the horizontal and the line of sight that connects an observation point to an elevated object.
- The angle of Depression– The depression angle is the angle formed by the horizontal and the line of sight from an observation point to an item below the horizontal level.
- Definition of Depression Angle
When we glance down, it measures the change in angle of our vision. Assume you’re standing in your kitchen, straightening your gaze, when you notice an insect creeping across the floor. So, the angle of depression is that sudden change in your vision from straight to downwards.
The angle of depression is calculated using the same formula as fundamental trigonometric ratios. If we know the lengths of any two of the right triangle’s sides, we can simply calculate the requisite angle using the angle of depression calculations listed below.
- Angle of Elevation vs. Angle of Depression
The angles of depression and elevation are diametrically opposed. The object is put below the spectator in the angle of depression, whereas it is positioned above the observer in the angle of elevation. The angle of elevation will be produced if you are standing on your terrace and staring at the sun. On the other hand, if you look at the dog on the road from your terrace, you will notice an angle of depression. The heights and lengths are calculated using trigonometry angles in both cases.
- Angle of Depression in a Triangle
The angle of depression in a right-angled triangle is produced at the top of the perpendicular line segment. It is originally on the outside of the triangle, but we can compute its alternate angle inside the triangle using the alternate interior angles theorem.
Let’s discuss it by an example:
Question – Find the value of x in the given figure.
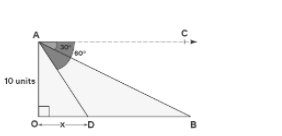
Ans – ∠BAC=30° and ∠DAC=60°, respectively, are two angles of depression created from point A in the diagram above. We already know that ∠DAC=∠ADO (by using alternate interior angles theorem). As a result, ∠ADO=60°. We derive tan 60° = AO/OD by using the angle of depression formula in triangle AOD.
- √3 = 10/x
- x = 10/√3 units
- As a result, x has a value of 10/√3 units.
Conclusion:
When an observer looks down at an object, the angle of depression is generated. It is the angle created by the line of sight and the horizontal line that is straight to the observer’s eye.The depression angle is now defined as the angle produced between the observer’s horizontal plane and the line of sight. The unimpeded vision or a line that connects both the observer and the object is referred to as this line of sight. The depression angle is a useful tool for resolving common issues. If we know the height and angle of depression, we can utilize it in trigonometric applications to compute the distance between the observer and the object.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out



