A probability tree diagram is a visual depiction of the probabilities and outcomes of an event. There are two pieces to a probability tree diagram: nodes and branches. An event is represented by a node. The term “branch” refers to the link between an occurrence and its result. A probability tree diagram can be used to represent both conditional and independent probabilities.
Definition of Probability Tree
The chance of events occurring is represented using a probability tree diagram rather than elaborate calculations. It shows all of the probable outcomes of a situation. A probability tree’s objective is to display all of the possible outcomes of an event and compute the likelihood of each one. A probability tree diagram can be used to illustrate conditional probabilities or to show a succession of independent occurrences.
Component of the Probability Tree Diagram
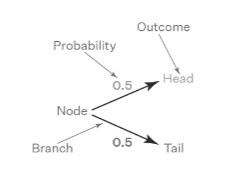
A probability tree has two primary components. The nodes and branches are these. The nodes can be further divided into parent and sibling nodes. The parent node denotes a specific occurrence with a probability of one. Other alternative occurrences or consequences are represented by the sibling nodes. The branches represent the likelihood of these occurrences occurring. If a fair coin is tossed once, the following probability tree may be constructed:
This is a straightforward probability tree with only two branches. The parent event of a coin toss is represented by the first node. The two potential outcomes that make up the sibling nodes are head and tail. The likelihood of each sibling event occurring is represented by the number 0.5 on the branch.
Example of a Probability Tree Diagram:
Assume you need to create a probability tree diagram for flipping a fair coin twice. Because the outcome of each coin toss is independent of the preceding flip, this is an example of an independent event. To begin, construct the probability tree diagram of a coin-flipping once as shown in the previous section. The next stage is to increase the number of coin tosses to two:
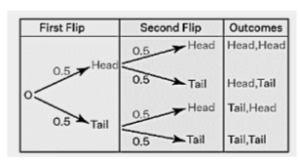
The second coin flip is represented by the second set of probability. As a result, there are four possible outcomes.
Multiply the probabilities along the branches of the probability tree diagram to compute the possibilities of a series of occurrences. The overall likelihood may be calculated by putting these probabilities together, and the result will always be 1.
The probability tree diagram may be used to make the following inferences:
- The chances of receiving the result (Head, Head) are 0.5 x 0.5 = 0.25. The likelihood of the other eventualities may be computed in the same way.
- 0.25 + 0.25 + 0.25 + 0.25 Equals 1. This means that when the odds of each scenario are added together, the total equals 1.
- The chance of receiving exactly one head may be estimated using the probability tree as 0.25 + 0.25 = 0.5.
Diagram of a Conditional Probability Tree:
The result of dependent events can be shown using a conditional probability tree diagram. A dependent event is one in which the result is influenced by a prior occurrence. Assume a student is required to take two tests. The chances of his passing the first test are 0.7. If he passes the first test, he has a 0.8 chance of passing the second. Furthermore, if he fails the first test, he has a 0.6 chance of passing the second. The probability tree diagram may be made using the procedures below to obtain the conditional likelihood that he will fail both tests.
Step 1: For the first test, create a probability tree diagram. Because the chance of passing the first test is 0.7, the chance of failing is 1 – 0.7 = 0.3.
Step 2: If the student passes the first test, construct branches for the second test. It’s worth noting that the total of result probabilities, 0.8 + 0.2, equals 1.
Step 3: Now, if the student fails the first test, design branches for the second test.
Step 4: To acquire the conditional probability results, multiply the probabilities along each branch of the probability tree.
Building Probability Tree:
To build a probability tree diagram, you must first determine all conceivable outcomes and their corresponding probabilities. The following are the stages of making a probability tree:
- Step 1: Determine if the occurrences are dependent or independent in the first step.
- Step 2: To illustrate the first set of outcomes, draw branches.
- Step 3: On the branch, write the probabilities associated with each result.
- Step 4: Determine if the upcoming occurrences are dependent or independent and draw the next set of branches. Include the corresponding probability as well.
- Step 5: Repeat step 5 as many times as necessary.
- Step 6: The probabilities along the branches must be compounded to obtain the overall probability of the probability tree. The total of these probabilities should never be less than one.
Conclusion:
In probability theory, a tree diagram can be used to depict a probability space. Tree diagrams can be used to illustrate a succession of independent events (such as a series of coin flips) or conditional probabilities (such as drawing cards from a deck, without replacing the cards). Each node in the diagram represents an event and is connected with a probability. The root node has probability 1 since it represents a certain occurrence. Each sibling node represents a full and distinct split of the parent event.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out