Introduction:
Definition of Interior Angle
The angles formed on the opposite sides of the transversal can be called alternate interior angles. In other words, eight angles are generated when two parallel lines are intersected by a transversal. The alternate interior angles are the angles that are on the inner side of the parallel lines but on the opposite sides of the transversal.
When a transversal crosses two parallel lines, the pair of angles formed on the inner side of the parallel lines but opposing sides of the transversal is referred to as alternate interior angles. These angles are always in the same proportion. This can also be interpreted differently. The alternate angles can be used to find the given lines are parallel or not. The given lines that are crossed by a transversal are said to be parallel if these angles are equal. When a transversal connects two coplanar lines, alternate interior angles are generated. They are on the inner side of the parallel lines but on the transversal lines’ opposing sides. The transversal runs between two parallel lines that are coplanar at different locations. These angles indicate whether or not the two supplied lines are parallel to one another. When these angles are equivalent, the lines that the transversal crosses are parallel.
Alternate Interior Angle
The alternate interior angles can be seen in the diagram below. l and m are two parallel lines that are intersected by a transversal line t.
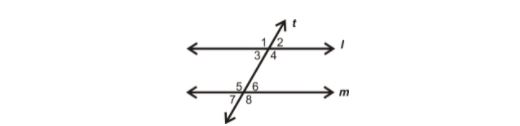
The pairs of alternate interior angles in the above figure, according to the alternate interior angles theorem, are:
∠4 and ∠5
∠3 and ∠6
Let’s take a quick look at alternate external angles and how they differ from alternate interior perspectives.
Alternate Exterior Angle
Angles with distinct vertices, lying on opposite sides of the transversal, and being external to the lines are known as alternate exterior angles. The alternate exterior angles created when a transversal intersects two parallel lines are always equal. The pairs of alternate exterior angles in the same figure are 1 & 8 and 2 & 7.
The Converse of Alternate Interior Angles Theorem
If a transversal intersects by two lines such that the alternate interior angles are the same or equal, the two lines are said to be parallel, according to the converse of the alternate interior angles theorem.
What Is the Best Way to Find Alternate Interior Angles?
According to the alternate interior angles theorem, the alternate interior angles of two parallel lines are equal. We take advantage of this fact to come up with new interior angles.
Let us take an example to understand this clearly, in the map below, the road designated Sixth Avenue runs perpendicular to the parallel streets of 1st Street and 2nd Street. Another route, Maple Avenue, forms a 40-degree angle with 2nd Street. calculate the angle x’s measurement?
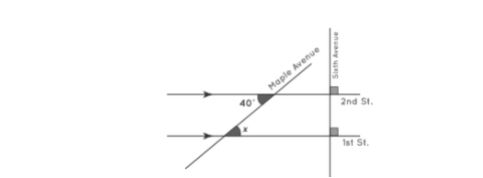
Let us Calculate the above Problem, If the two streets are parallel and Maple Avenue is regarded as the transversal, then x and 40° are the alternate interior angles, according to the alternate interior angles theorem. As a result, both angles are equal. As a result, x = 40°.
Important Reminders:
- Each alternate interior angle pair is the same.
- Each pair of co-interior angles adds to give 180 degrees.
- Each corresponding angle pair is the same.
- Each alternate pair of external angles is the same.
- Alternate Interior Angles are two angles on the inner side of each of those two lines but separate sides of the transversal.
- When a transversal travels through two lines, it creates alternate interior angles. Alternate interior angles are generated on opposite sides of the transversal and inside the two lines.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






