Profile
Settings
Refer your friends
Sign out
The triangle law of vector addition is a mathematical concept that is used to compute the sum of two vectors in two-dimensional space. In order to add two vectors, the first vector’s head is linked to the tail of the second vector, followed by attaching the tail of the first vector to the head of the second vector to form a triangle, thus obtaining the resultant sum vector, this law is applied. As a result, the triangle law of vector addition is sometimes referred to as the head-to-tail approach for the addition of vectors in some circles.
The triangle law of vector addition, its statement, formula, and proof will all be covered in this section. Net displacement, velocity, acceleration, and other parameters are calculated using this law. We will also work through problems and examples that are based on the triangle law of vector addition in order to better grasp its application and conceptualization.
Triangle Law of Vector Addition
It is possible to utilise the triangle law of vector addition in vector algebra to compute the resultant sum vector when two or more vectors are added together. Assume we have an automobile that is going from point A to point B, as seen in the diagram to the right. Once it reaches point B, it resumes its journey until it reaches point C. Now, in order to calculate the net displacement of the car, we will employ the notion of vector addition. The net displacement of the car is given by the vector AC, which may be calculated using the triangle rule of vector addition, as shown in the following example:
AC=AB+BC
Similarly, if we have two vectors P and Q, as shown below, and we need to compute their sum, we can move the vector Q in such a way that its tail is attached to the head of the vector P without changing its magnitude or direction. Then, using the triangle law of vector addition, we can compute the sum of the vectors P and Q as follows:
R=P+Q
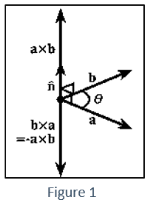
Cross Product Example
Example:
Any three points in the plane define a plane. If the plane contains points P(1,0,0), Q(1,1,1) and R(2,-1,3) Find a vector that is orthogonal to the plan.
Solution:
Taking the cross product is the only way to get an orthogonal vector. Therefore, if we can find two vectors that are known to be in the plane and take the cross product of those two vectors, we know that the cross product is orthogonal to both vectors. However, because both vectors are in the plane, the cross product is also orthogonal to the plane.
As a result, we require two vectors in the plane. Since all three points are in the plane, the vector between them must also be in the plane. There are numerous methods for obtaining two vectors between these points.
The Difference Between Cross Product and Dot Product
Cross product | Dot product |
The cross-product is the sum of the magnitudes of the vectors and the sine of the angle at which they intersect. | The dot product is made up of the magnitude of the vectors and the cosine of the angle between them. |
A vector quantity is the result of the vectors’ cross-product. | The dot product of the vectors yields a scalar quantity. |
A vector is returned by the cross product. | A number is produced by the dot product. |
The cross product of two vectors A and B is written as Α × Β = ΑΒ sin θ | The dot product of two vectors A and B is written as. Α.B = ΑΒ cos θ |
Cross product works only in 3D. | Dot product works in any dimension. |
When the vectors are orthogonal (θ= 90 °), the cross product is greatest. | The dot product is zero if the vectors are orthogonal (θ = 90 °). |
The commutative law does not apply to the cross product of two vectors. A × B ≠ B × A | The commutative law governs the dot product of two vectors. |
Conclusion
In this article we conclude that The cross product is a type of measure of the dot product, which is the measure of “equivalence” between two vectors, whereas the difference is the measure of “difference” between two vectors. For the cross product, the more vertical the two vectors are, the larger the cross product will be. If the two vectors are parallel, this “difference” measurement is zero. This “difference” measure, which is the product of the magnitudes of the two vectors, is the largest if they are perfectly vertical. It also points in the farthest direction in a sense from the two vectors. The main uses of the cross product are the calculation of the angle between two vectors, the calculation of the moment of the force around the point, as well as the determination of the vector perpendicular to the plane.
