The triangle law of vector addition is a mathematical concept that is used to compute the sum of two vectors in two-dimensional space. In order to add two vectors, the first vector’s head is linked to the tail of the second vector, followed by attaching the tail of the first vector to the head of the second vector to form a triangle, thus obtaining the resultant sum vector, this law is applied. As a result, the triangle law of vector addition is sometimes referred to as the head-to-tail approach for the addition of vectors in some circles.
The triangle law of vector addition, its statement, formula, and proof will all be covered in this section. Net displacement, velocity, acceleration, and other parameters are calculated using this law. We will also work through problems and examples that are based on the triangle law of vector addition in order to better grasp its application and conceptualization.
Triangle Law of Vector Addition
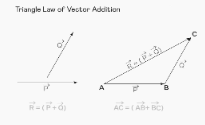
It is possible to utilise the triangle law of vector addition in vector algebra to compute the resultant sum vector when two or more vectors are added together. Assume we have an automobile that is going from point A to point B, as seen in the diagram to the right. Once it reaches point B, it resumes its journey until it reaches point C. Now, in order to calculate the net displacement of the car, we will employ the notion of vector addition. The net displacement of the car is given by the vector AC, which may be calculated using the triangle rule of vector addition, as shown in the following example:
AC=AB+BC
Similarly, if we have two vectors P and Q, as shown below, and we need to compute their sum, we can move the vector Q in such a way that its tail is attached to the head of the vector P without changing its magnitude or direction. Then, using the triangle law of vector addition, we can compute the sum of the vectors P and Q as follows:
R=P+Q
The formula for the Triangle Law of Vector Addition
In this case, consider two vectors P and Q with a difference in angle between them, and the resultant sum vector obtained by using the triangle law of vector addition is represented by the vector R. The following is the formula for the magnitude |R| and direction of the resultant vector R obtained by applying the triangle law for the addition of vectors:
|R| = √(P² + Q² + 2PQ cos θ)
ϕ = tan-¹[(Q sin θ)/(P + Q cos θ)]
Proof of the Triangle Law of Vector Addition
Before proceeding to the proof of the triangle law of vector addition, let us first consider the statement of the triangle law of vector addition:
A statement is true if two vectors acting on a body at the same time are represented both in magnitude and direction by two sides of a triangle taken in order, and the sum vector (both in magnitude and direction) of these two vectors is given by the third side of that triangle taken in the opposite order of the two vectors.
Consider the following two vectors P and Q, whose magnitudes are indicated by the sides OA and AB, respectively, in the diagram below: P and Q. Now, using the triangle law of vector addition, the sum of these vectors is provided by the resultant vector R (side OB of the triangle), whose magnitude and direction are also given by the original vectors.
|R| = √(P² + Q² + 2PQ cos θ)
ϕ = tan-1[(Q sin θ)/(P + Q cos θ)]

Now, extend the side OA till point C, so that BC is perpendicular to OC and the angle between vectors P and Q is equal to the angle between the vectors P and Q. Aside from that, the angle indicates the direction in which the resultant vector R will point. We have a right-angled triangle OBC in our example.
OB² = OC² + BC²
⇒ OB² = (OA + AC)² + BC² — (1)
In the right triangle ABC, we have
cos θ = AC/AB and sin θ = BC/AB
⇒ AC = AB cos θ and BC = AB sin θ
⇒ AC = Q cos θ and BC = Q sin θ — (2)
Substituting values from (2) in (1), we have
R² = (P + Q cos θ)² + (Q sin θ)²
⇒ R² = P² + Q²cos2θ + 2PQ cos θ + Q²sin2θ
⇒ R² = P² + 2PQ cos θ + Q²(cos2θ + sin2θ)
⇒ R² = P² + 2PQ cos θ + Q²[cos2θ + sin2θ = 1]
⇒ R = √(P² + 2PQ cos θ + Q²) → Magnitude of the resultant vector R
Now, to find the direction of R, we have in right triangle OBC,
tan ϕ = BC/OC
⇒ tan ϕ = Q sin θ/(OA + AC) [From (2)]
⇒ tan ϕ = Q sin θ/(P + Q cos θ) [From (2)]
⇒ ϕ = tan-1[(Q sin θ)/(P + Q cos θ)]
The direction of the resulting vector R is denoted by
So, we’ve established the formulas for the triangle law of vector addition and demonstrated it.
Important Points to Remember About the Triangle Law of Vector Addition
When the head of the first vector is joined to the tail of the second vector, the triangle law of vector addition can be utilised to compute the sum of the two vectors that have been linked.
The magnitude of the resulting sum vector R is given by the formula: R = (P2 + 2PQ cos + Q2)
The following is the direction of the resulting vector R:ϕ =tan-1[(Q sin θ)/(P + Q cos θ)]
Conclusion
The triangle law of vector addition is a mathematical concept that is used to compute the sum of two vectors in two-dimensional space. In order to add two vectors, the first vector’s head is linked to the tail of the second vector, followed by attaching the tail of the first vector to the head of the second vector to form a triangle, thus obtaining the resultant sum vector, this law is applied. It is possible to utilise the triangle law of vector addition in vector algebra to compute the resultant sum vector when two or more vectors are added together. When the head of the first vector is joined to the tail of the second vector, the triangle law of vector addition can be utilised to compute the sum of the two vectors that have been linked.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






