A geometric progression (GP) is one in which each term has a constant ratio to the one before it. It’s a unique kind of progression. We must multiply with a fixed term known as the common ratio every time we want to find the next term in the geometric progression, and we must divide the term with the same common ratio every time we want to find the preceding term in the progression. Any two consecutive numbers in a G.P. have the same ratio, which we call the constant ratio. The letter ‘r’ is usually used to represent it. As a result, if we have a G.P.
Finite or infinite geometric progressions are possible. Its common ratio can be either positive or negative.
Geometric Sequence Definition
A geometric sequence, also called a geometric progression, is a non-zero number sequence in which each term after the first is found by multiplying the previous one by a fixed, non-zero number called the common ratio.
Geometric Progression
A geometric progression is a type of progression in which each term has a fixed ratio known as the common ratio. GP is another name for it. The GP is usually written as a, ar, ar2…, where an is the first term and r is the progression’s common ratio. Both negative and positive values are possible for the common ratio. We only need the first term and the constant ratio to find the terms of a geometric series.
There are two types of geometric progression.
- Finite geometric progression: There are a finite number of terms in a finite geometric progression. It is at this point in the progression that the last term is defined.
- Infinite geometric progression: There are an infinite number of terms in an infinite geometric progression. It’s a progression in which the last term is not specified.
Example: For example, the geometric sequence 1, 2, 4, 8, 16, 32… has a common ratio of r = 2.
Geometric Progression Formula
To find the nth term in a progression, use the geometric progression formula. We need the first term and the common ratio to find the nth term.
If you don’t know what the common ratio is, you can figure it out by multiplying any term by its preceding term. The formula for the geometric progression’s nth term is:
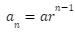
In this formula:
The first term is a.
The common ratio is r.
n is the number of the term we’re looking for.
Sum of Geometric Progression
To find the sum of all the terms in a geometric progression, use the geometric progression sum formula. Because geometric progression is divided into two types, finite and infinite geometric progressions, the sum of their terms is calculated using different formulas.
If a geometric progression has a finite number of terms, the sum of the geometric series is calculated using the formula:
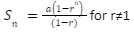
,where the first term is a.
The common ratio is r.
The number of terms in the series is n.
An infinite geometric series sum formula is used when the number of terms in a geometric progression is infinite.
When |r| < 1
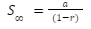
When |r| > 1
The series does not converge; it diverges and has no sum in this case.
Conclusion
In this article we conclude that, if each term after the first is obtained by multiplying the preceding term by a constant quantity, a sequence of non-zero numbers is said to be in Geometric Progression abbreviated as G.P.Positive or negative. The constant ratio, also known as the Geometric Progression’s common ratio, is calculated by dividing any term by the term immediately preceding it. Mathematicians use geometric series all the time. Physics, engineering, economics, computer science, queuing theory, and finance all benefit from them.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






