When a function changes with regard to an independent variable, it is said to be deriving from that function at a variable rate. Typically, the derivative is employed when there is a variable quantity and the rate of change is not constant. The derivative is a mathematical concept that is used to quantify the sensitivity of one variable (dependent variable) to another one (independent variable).
Derivatives in Maths
In mathematics, the term derivative refers to the instantaneous rate of change of one quantity in relation to the other. It is useful in determining the nature of an amount on a moment-to-moment basis.
Differentiation is the term used to describe the process of determining the derivative. Anti-differentiation is the term used to describe the inverse process. Calculate the derivative of a function with coefficients of proportionality y = f(x). When the value of the variable x changes, it is the rate at which the value of y changes in relation to the change of the variable. The derivative of the function “f” with regard to the variable x is referred to as the derivative of the function “f.”
An infinitesimal change in x is represented by the symbol dx, while the derivative of y with respect to x is denoted by the symbol dy/ dx.
The derivative of y with respect to x is written as “dy by dx” or “dy over dx” in this context.
Example:
Consider the variables ‘y’ and ‘x’ to be dependent variables and independent variables, respectively.
Consider the effect of a change in the value of x, denoted by the symbol dx. This change in x will result in a change in y, which will be denoted by the letter dy.
Using the following formula, we can calculate the change in y when the unit change in x is increased by one:
Let f(x) be a function whose value varies in proportion to the variation in the value of x.
Steps to Find the Derivative
Change x to the smallest possible value and call it ‘h,’ resulting in the function f(x+h) instead of f(x).
Calculate the change in the value of a function, which is: f(x + h) – f(x)
The rate of change in function f(x) when the variable ‘x’ is changed to ‘x+h’ will be
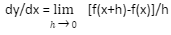
Now, d(x) is thought to be ignorable because it is deemed to be too little.
Derivatives Formulas
The following are the derivative formulas for some of the functions, including linear, exponential, and logarithmic functions:
d/dx (k) = 0, where k is any constant
d/dx(x) = 1
d/dx(xⁿ) = nxⁿ⁻¹
d/dx (kx) = k, where k is any constant
d/dx (√x) = ½√x
d/dx (1/x) = -1/x²
d/dx (log x) = 1/x, x > 0
d/dx (eˣ) = eˣ
d/dx (aˣ) = aˣ log a
Types of Derivatives
First and second order derivatives are two types of derivatives that can be classified based on the order in which they are executed. These can be defined in the following manner.
First Order Derivative
The direction of the function is indicated by the first order derivatives, which indicate whether the function is increasing or decreasing. The first derivative maths, also known as the first-order derivative, can be thought of as a rate of change that occurs instantly. The slope of the tangent line can also be used to predict the result.
Second Order Derivative
Using second-order derivatives, we can get an understanding of the shape of the graph corresponding to the provided function and its derivatives. Concavity is a property of functions that can be used to classify them. The concavity of the provided graph function can be divided into two categories, which are as follows:
Concave up
Concave down
Calculus – Derivative Example
Consider the function f(x), where f(x) = x².
The derivative of x² is 2x, which means that for every unit change in x, the value of the function increases by twice as much as it decreases (2x).
Calculus – Derivative Example
When dx is reduced to such a small value that it almost becomes insignificant. When we say that x approaches zero but does not reach zero, we are referring to the concept of Limits.
Key Concepts
Before attempting to discriminate between two powers of x that are in the denominator, represent the power in the denominator as a power with a negative exponent. Eg.
1/x² = x⁻²
The process of differentiating polynomial functions is made easier by using derivative rules.
If you want to distinguish between two radicals, first express them as powers with a reasonable exponent.
Derivatives of Trigonometric Functions
We can also discover the derivative of trigonometric functions, which means we can find the derivative of sin, cos, tan, and other functions. The following formulas are provided:
d/dx (sin x) = cos x
d/dx (cos x) = -sin x
d/dx (tan x) = sec²x
d/dx (cosec x) = -cosec x cot x
d/dx (sec x) = sec x tan x
d/dx (cot x) = -cosec²x
Properties of Derivatives
Derivatives can be broken into smaller sections so that the provided expressions can be conveniently assessed. In the process of splitting the expressions or functions, the terms are separated based on the operator such as plus (+), minus (-) or division (/).
Derivatives Examples
Example 1: Find the derivative of 2 tanx + 1.
Solution: Let the given function be f(x) = 2 tan x + 1
Now, taking the derivative,
d/dx f(x) = d/dx (2 tan x + 1)
= d/dx (2 tan x) + d/dx (1)
= 2 (sec²x) + 0
= 2 sec²x
Conclusion
Diverse applications of derivatives can be found not only in mathematics and real life, but also in a wide range of other fields such as science, engineering, physics, and so on. To use graphs to calculate the profit and loss in a business venture. In order to determine the temperature variation. To calculate the speed or distance travelled, such as miles per hour, kilometres per hour, or kilometres per hour. In physics, derivatives are used to derive a large number of equations. In the field of seismology, it is common practice to determine the magnitude range of an earthquake.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






