A function is said to be continuous if it can be drawn without the need to pick up a pencil at any point in the process. A function is said to be discontinuous if this is not the case. The same is true in mathematics. A function f(x) is continuous at the point x=c if the graph of the given function does not contain any breaks at that point (in other words, it is not discontinuous). The letter c, the letter f(c)). In this article, we will cover the continuity and discontinuity of a function, as well as the various forms of continuity and discontinuity, as well as circumstances and illustrations.
Continuity Definition
A function is considered to be continuous in a certain interval if the graph of the function does not show any discontinuities throughout the whole interval range. In this example, consider the real function on a subset of the real numbers, with “c” representing a point in the domain of f. F is continuous at c if and only if
limx→c f(x) = f(c)
If the left- and right-hand limits, as well as the value of the function at x = c, all exist and are equal to each other, this is known as a closed-form solution.
limx→c⁻ f(x) = f(c) = limx→c⁺ f(x)
When x = c, f is said to be continuous.
Conditions for Continuity
An open interval (a, b) is said to be continuous if and only if the function “f” is continuous at each point in the interval.
When a function “f” is continuous in a closed interval [a, b], it is said to be continuous in the interval [a, b].
f is continuous in (a, b)
limx→a⁺ f(x) = f(a)
limx→b⁻ f(x) = f(b)
Some Typical Continuous Functions
Trigonometric Functions in certain periodic intervals (sin x, cos x, tan x etc.)
Polynomial Functions (x² +x +1, x⁴ + 2….etc.)
Exponential Functions (e2x, 5ex etc.)
Logarithmic Functions in their domain (log10x, ln x2 etc.)
Continuity Over an Interval
Following our exploration of the concept of continuity at a specific location, we will now expand that concept to the concept of continuity over an interval. Keeping in mind the intuitive sense that a function is continuous over an interval if we can use a pencil to draw the function between any two places in the interval without lifting the pencil off of the paper may be helpful as we develop this concept for different sorts of intervals. For the purpose of defining continuity on an interval, we first examine the concept of what it means for a function to be continuous from the right at a point and continuous from the left at a point in order to prepare for that definition.
An open interval is continuous if and only if a function is continuous at every point in the interval. A function f ( x ) is continuous over a closed interval of the type [ a, b ] if and only if it is continuous at every point in ( a, b ) and is continuous from the right at a and is continuous from the left at b ; otherwise, it is discontinuous over the interval. For analogy’s sake, an interval of the form (a, b) is continuous over a function of the form (f (x) when the function f (x) is continuous over the interval (a, b) and is continuous from the left at b. Continuousness across different types of intervals is defined in a similar manner to continuousness over time.
Discontinuity Definition
If any of the following conditions are met, the function “f” will be discontinuous at x = a:
f (a) is not defined.
limx→a⁻ f(x) and limx→a⁺ f(x) exist but are not equal.
limx→a⁻ f(x) and limx→a⁺ f(x) exist and are equal but not equal to f(a).
Types of Discontinuity
In this section, we will discuss the three main forms of discontinuities that exist:
Removable Discontinuity
Jump Discontinuity
Infinite Discontinuity
Removable Discontinuity
An example of detachable discontinuity is a function that has clearly delineated bilinear limits at the point x=a, but in which f(a) is either not defined or not equal to its limits. The following is an example of a detachable discontinuity:
limx→a f(x) ≠ f(a)
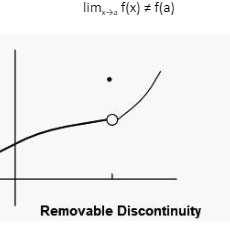
This type of discontinuity can be readily addressed by redefining the function in such a way that it no longer contains any discontinuities.
f(a) = limx→a f(x)
Jump Discontinuity
It is a type of discontinuity in which the left-hand limit for a function x = a and the right-hand limit for the same function x = an exist, but they are not equal to each other. Jump Discontinuity is defined as follows: The discontinuity caused by the jump can be expressed as follows:
limx→a⁺ f(x) ≠ limx→a⁻ f(x)
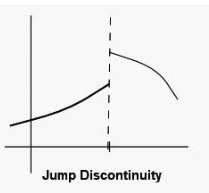
Infinite Discontinuity
When there is an infinite discontinuity, the function diverges at x =a, resulting in a discontinuous nature being revealed. In this case, it signifies that the function f(a) has not been defined. It is also not known how far the value of the function at x = a will go before it reaches a finite value or if it will reach infinity.
Conclusion
In order to establish whether numerical approaches will be effective in locating the root of a function or not, continuity must be considered. Differentiability is used in a similar way to the previous two concepts. Differentiability is an important technique in the study of functions, and it can be used to discover the minima and maxima of a function, for example.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






