Watch Free Classes

Vector algebraic ideas such as collinear vectors are considered to be amongst the most essential in the field. A collinear vector is a vector that occurs when two or more of the supplied vectors occur along the same line in the same direction as one another. Two parallel vectors might be considered collinear vectors since they are pointing in the same direction or in the opposite direction of each other.

Collinear vectors, their definition, and the conditions of vector collinearity will be covered in this article, along with cases that have been solved for you.

Collinear Vectors

Whenever any two provided vectors are parallel to the same given line, they can be considered to be collinear vectors. To put it another way, we can consider any two vectors to be collinear when they are either along the same line or parallel to one another. A scalar multiple of another vector is required for any two vectors to be parallel to one another, and this is the requirement for any two vectors to be parallel to one another.

tf1

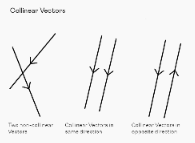
The vectors that are parallel to the same line are collinear to each other in the diagram above, and the vectors that intersect are non-collinear vectors.

Collinear Vectors Under Specific Conditions

A set of conditions must be met by any two vectors in order for them to be considered to be collinear. The following are the critical criteria for vector collinearity:

  • (1) Two vectors p and Q are deemed to be collinear vectors if there is an integer “n” such that the product of the two vectors is equal to the product of the two vectors.
  • 2. A pair of collinear vectors (p and q) are considered to be collinear vectors when and only when their corresponding radial coordinate ratios are equal. It is not possible to satisfy this condition if any one of the components of the provided vector equals zero.
  • The condition 3 is met when the cross product of two vectors p and q is identical to the zero vector, which is called a collinear vector. This criterion can only be used for issues that are three-dimensional or spatial in nature.

Important Points to Remember About Collinear Vectors

There are several points that should be kept in mind when studying collinear vectors, which are listed below.

Whenever any two provided vectors are parallel to the same given line, they can be considered to be collinear vectors.

In this way, we can consider any two vectors to be collinear only when they are either along the same line or if they are parallel to each other in their direction of travel.

Conclusion

Whenever any two provided vectors are parallel to the same given line, they can be considered to be collinear vectors. To put it another way, we can consider any two vectors to be collinear when they are either along the same line or parallel to one another. A scalar multiple of another vector is required for any two vectors to be parallel to one another, and this is the requirement for any two vectors to be parallel to one another. A set of conditions must be met by any two vectors in order for them to be considered to be collinear. Whenever any two provided vectors are parallel to the same given line, they can be considered to be collinear vectors. In this way, we can consider any two vectors to be collinear only when they are either along the same line or if they are parallel to each other in their direction of travel.