Profile
Settings
Refer your friends
Sign out
An arithmetic progression is a numerical sequence or series in which each subsequent value is obtained by adding a constant to the first. The name given to this constant is the common difference. Because the last term in the sequence can be represented by an equation, such a numerical sequence is considered a progression. To find the sum of n terms in Arithmetic Progression, we must first comprehend this type of sequence, including its terminologies and formula.
The difference between any two consecutive numbers in an arithmetic progression (AP), also known as an arithmetic sequence, is always the same. 3, 6, 9, 12, 15… and 30 are some examples. Each number after that differs by three from the previous one. As a result, before determining whether the number series is in AP, we must first determine whether the difference between all of the terms is constant.
Definition of Arithmetic progression
“Arithmetic progression is a set of numbers in which the second is obtained by multiplying the first by a constant. The constant that must be added to any term of an AP to get the next term is called the common difference (C.F) of the arithmetic progression”.
Arithmetic Progression’s First Term
As the name implies, the first term of an AP is the progression’s first number. a1 (or) a is commonly used to represent it.
For example, the first term in the sequence 6,13,20,27,34,… is 6, i.e., a1=6 (or) a=6.
Arithmetic Progression in a More Generalized Form
Because the first term is “a” and the common difference is “d,” the next term should be a+d, and the next term after that should be a+d+d, and so on, a generalized way of representing the A.P. can be formed. The Arithmetic Progression is written like this:
a, a+d, a+2d, a+3d, a+4d, ………. a+ (n-1)d
The first term of the progression is represented by “a” and the common difference is represented by “d.”
The progression’s final term “an“ is written as,
nth Term of AP
The nth the term of an arithmetic progression is the term that appears in the nth position from the first (left side). An arithmetic progression is a sequence in which the differences between each pair of consecutive terms are the same. To find any term in AP (Arithmetic Progression), use the nth term. A term of AP is usually obtained by multiplying the common difference of AP by the previous term. However, we can find any term of AP using the nth term of the AP formula without knowing its previous term.
The formula an=a+(n-1)d is used to find the general term (or) nth term of an AP whose first term is ‘a’ and the common difference is ‘d’.
For example, we substitute the first term, a1=6, and the common difference, d=7 in the formula for the nth terms to find the general term (or) nth term of the sequence 6,13,20,27,34,…
After that, we get an=a+(n-1)d = 6+(n-1)7 = 6+7n-7 = 7n -1
As a result, the sequence’s general term (or nth term) is: an= 7n-1.
Sum of theFirst n Terms
An AP can have an infinite number of terms. The sum of an AP n terms can be easily measured using a simple formula that states that if the AP first term is a and the common difference is d, the AP sum of n terms is:
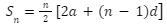
In other words, the formula for calculating the sum of an AP’s first n terms in the form “a, a+d, a+2d, a+3d,….., a+(n-1)d” is:
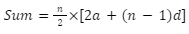
When the last term is given in AP, the sum of n terms is given:
When the nth term an, is known, the sum of the first n terms of an arithmetic progression is:
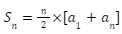
Example
Find the sum of the first 5 terms of an arithmetic progression with the first term 3 and the 5th term 11.
Solution:
Given a1=a=3 and a5=11 and n=5
We can calculate the sum of n terms using the AP formula.
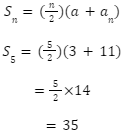
Answer: The sum of the first 5 terms must be 35.
Conclusion
We conclude in this article that an arithmetic progression is a set of terms with a common difference between them that is a constant value. It’s a term for a collection of patterns that we notice in our daily lives. In real life, the arithmetic sequence is important because it allows us to understand things through patterns. An arithmetic sequence can be used to describe a variety of things, including time, which has a common difference of one hour. Simulating systematic events also necessitates the use of an arithmetic sequence.
