Algebraic Integrals Forms

Integral calculus helps find the antiderivatives of a function. Antiderivatives are also called function integrals. Integration is the method of calculating a function’s antiderivative. The procedure of determining integrals is the inverse of determining derivatives. The integral function displays a curve family. The fundamental calculus entails calculating derivatives and integrals. This article covers the principles of integrals and how to assess integrals in this course.

Integral Calculus—Defined

Function values discovered during the integration process are known as integrals. Integration (x) is the method of deriving f(x) from f’. Integrals offer numbers to functions to represent displacement and motion issues, area and volume issues, and other issues that arise from combining all the little data. Using the derivative f’ of the function f, you can deduce the function f. In this case, the function f is called the antiderivative or integral of f’.

Example: 

Given: f(x) = x2

Derivative of f(x) = f'(x) = 2x = g(x)

if g(x) = 2x, then antiderivative of g(x) = ∫ g(x) = x2 

Integral Definition

F(x) is an antiderivative or Newton-Leibnitz integral or primal of a function f(x) on an interval I, with F'(x) = f(x) for all x values in I.

An integral represents the place below the region of the curve. You can approximate the true integral value by drawing a rectangle. 

A definite function of an integral is defined as the place of the region being bounded with the graph of the particular function taking place between the two straight lines. 

A region’s area is measured by splitting it into small vertical rectangles and setting lower and upper limits. The region’s area is then combined. You can define a function integral spanning an interval determined by the integral.

Integration Formulas

Integral equations, trigonometric ratios, inverse trigonometric functions, logarithmic and exponential functions, and other functions can all be integrated using integration formulas. The underlying functions for which the derivatives were generated are returned via function integration. These integration equations are used to get the antiderivative of a function. If you differentiate a function f in an interval I, you get a family of functions in I. You can determine the function f if you know the values of the functions in I. Integration is the name given to this inverse differentiation method. You can take it a step further and look at the integration formulas used in integration procedures.

What Are Integration Formulas?

The integration formulas are the six sets of formulas shown below.

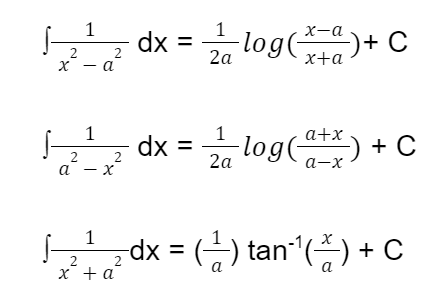
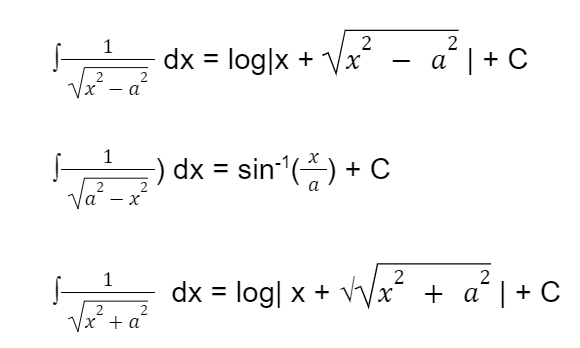
Essentially, integration is a method of connecting parts to form a whole. Basic integration formulas, integration of trigonometric ratios, inverse trigonometric functions, the product of functions, and some advanced integration formulas are among the formulas. 

Differentiation is the opposite process of integration. As a result, the fundamental integration formula is

∫ f'(x).dx = f(x) + C

Indefinite Integrals

Indefinite integrals are those that do not have upper or lower bounds. They may be expressed mathematically as follows:

∫f(x)dx = g(x) + C

The function f(x) is referred to as the integrand, and C is a constant.

Characteristics of Indefinite Integrals

The integrand is the derivative of an integral. ∫ f(x) dx = g(x) +C.

Given that two indefinite integrals with the same derivative produce the same family of curves, they are considered comparable.

∫ [ f(x) dx – g(x) dx] =0

The sum or difference of the integrals of a finite number of functions equals the sum or difference of the integrals of the individual functions. This may be mathematically expressed as: 

∫ [ f(x) dx +g(x) dx] = ∫ f(x) dx + ∫ g(x) dx

The constant multiplied with the function is taken out of the integral.∫ k f(x) dx = k ∫ f(x) dx, where k ∈ R.

The form is arrived at by combining the previous two attributes:

 ∫ [k1f1(x) + k2f2(x) +… knfn(x)] dx = k1∫ f1(x)dx + k2∫ f2(x)dx+ … kn ∫ fn(x)dx

Conclusion 

While these three concepts are still connected, they are not interchangeable in the same way that they are in the single-variable case. The concept of integration on forms is fundamental in differential topology, geometry, and physics, and it also yields one of the most important examples of cohomology, namely de Rham cohomology. 

It measures how far the fundamental theorem of calculus fails in higher dimensions and on general manifolds.