Absolute Value Functions

A function in mathematics is a relationship between a group of inputs with one output. A function, in simple terms, is a relationship between inputs in which each input is associated with only one output. Each function has a domain and a co-domain, often known as a range. The general notation is f(x), where x represents the input. A function’s general representation is y = f(x). 

Here, we’ll learn about Absolute Value Functions

Absolute Value Function is a function which gives non negative values of any number if we give input as any real no. Such functions are known as absolute value functions. It gives us the magnitude of any variable or number. Before diving more into the topic, lets have a quick understanding about functions. In order to express function in mathematical terms, transformation/mapping is applied to it. The visual representation of functions is generally done by alphabets like f, g, h., etc.

f(x)=x²

f:function name

x:input

x²:what to output

There are different types of functions in mathematics like

Polynomial Function,  Trigonometric Functions, Exponential Functions, Logarithmic, Implicit Function, Inverse Trigonometric Functions signum,

ABSOLUTE VALUE FUNCTION FORMULA

The function f(x)=|x| is called an absolute value function.

This demonstrates that the absolute value function catches the actual value if x holds a value equivalent to or greater than zero, but if x is less than 0 then function picks minus times the actual value of the original.

f(x)=|x| = {x 😡 > 0}

{-x 😡 < 0}

PROPERTIES OF Modulus FUNCTION

For any real number x, we have:

√x=|x|

||x||=|x|

If a and b denote positive real numbers, then:

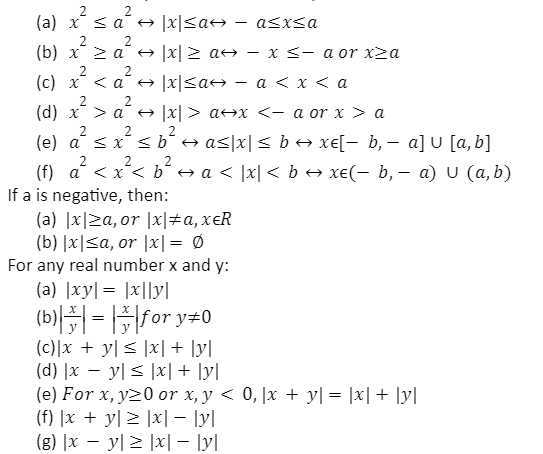
The absolute value of a positive number is positive. The absolute value of a negative number is obtained by ignoring the minus sign. Thus, the modulus function always possesses non-negative values.

DIFFERENTIATION OF ABSOLUTE VALUE FUNCTION:

Since we know that an absolute value function f(x)=|x| is equal to x if x>0 and-1 if x<0. The derivative of the absolute value function is not defined for x=0. Hence the derivative of absolute value function is x/|x|, x not equal to 0. Absolute value function x is not differentiable at x=0 as the graph of Mod(x) has a sharp point at x=0. Also, the left-hand limit and the right-hand limit are not equal at x=0. Absolute value function problems can be solved by applying modulus to a non-negative number and a negative number always results in the same number.

INTEGRATION OF ABSOLUTE VALUE FUNCTION:

The integral of x depends on the domain in which it is being      integrated.

For x>0, |x|=x.

For x<0, |x|=-x.

The integration of the modulus function can be clubbed as:

If |x| is integrated into the positive domain, the result obtained is:

CONCLUSION:

In this article,  study material notes on Absolute Value Function, we learned about the absolute value function along with its definition, domain and range of modulus function, followed by differentiation and integration of modulus function. With the help of absolute value function study material, we also studied about the properties of absolute value function, derivative and integral of modulus function and integration of modulus function. To gain a better understanding of this chapter, we strongly reccommend to revise other sub topics such as representation of functions by mapping, different types of functions, odd and even functions, many-one function, onto function and into function.