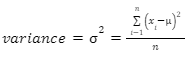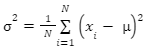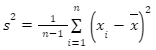A Study on the Variance Deviation for Grouped and Ungrouped Data

The variance formula in probability theory and statistics calculates how widely distributed a set of numbers is. It is a numerical value used to describe how far members of a group differ from one another. The variance is large if individual observations deviate significantly from the group mean, and vice versa. Variance is a crucial tool. The variance, also known as the second central moment of a distribution and the covariance of the random variable with itself, is equal to the standard deviation squared.

When the variance is 0, all the values are the same. A small variance shows that the data points tend to be relatively close to the mean and hence to each other, whereas a high variance suggests that the data points are widely dispersed both from the mean and from one another. It should be emphasised that variance is always non-negative.

We will learn about variance deviation in this article, along with the variance deviation of both grouped and ungrouped data.

Variance Deviation Definition

“Variance measures how far off data points are from the mean. Data points with low variation tend to be comparable to one another and deviate from the mean less frequently. High variance denotes greater variability and wider deviations from the mean in data values”.

How Do Find Out the Variance

We can compute the variance as follows:

1. Find the data set’s mean. Divide the total data values by the sample size, n.
2. For each data value, calculate the squared deviation from the mean. Square the result after deducting the mean from each data point.
3. Discover the total squared differences.
4. Do the variance calculation.

Formula of Variance

The sum of the squared deviations between each data point and the mean, divided by the number of data values, is the variance of a. The variance calculations in this calculator are done using the formulas below.

Variance Formulas for Ungrouped Data

For ungrouped data, population’s the variance is:

Where,

σ² denotes variance

x_i denotes ith observation of  data

μ denotes population mean

N denotes observations total no. 

For ungrouped data, the sample variance is:

s² Denotes sample variance  

x_i Denotes ith observation of data

n Sample size 

Variance Formulas for Grouped Data

For grouped data, a population’s variance is:

For grouped data, the sample variance is:

Where,

ƒ denotes frequency of the class 

m denotes midpoint of the class

Conclusion

In this article, we learned that Statistics’ use of variation is crucial because it enables us to calculate the spread of a group of variables around their mean. These variables make up the set that is being measured or examined. The variance serves as a good indicator of variability. If the scores in our sample of data are dispersed, the variance will be high. On the other hand, if the scores are evenly distributed around the mean, the variance will be lower. Variance matters for two reasons in particular: because they are sensitive to variance, for use with parametric statistical tests. The sample variances are used to determine if the populations the samples represent are distinct from one another.