A Study on Squeeze Theorem

The squeeze theorem is a theorem about the limit of a function caught between two other functions in calculus.

In calculus and mathematical analysis, the squeeze theorem is used to validate the limit of a function by comparing it to two other functions whose limits are known. It was initially utilised geometrically by the mathematicians Archimedes and Eudoxus in an attempt to compute, and Carl Friedrich Gauss defined it in contemporary terms.

The squeeze theorem is also known as the two officers theorem or a version thereof in several languages. According to the narrative, if two police officers are bringing an intoxicated prisoner between them to a cell, the prisoner must also end up in the cell.

Squeeze theorem or Pinch theorem are other names for the sandwich theorem. Using two functions in the neighbourhood, this is used to extrapolate the value of a function at a location x. The sandwich theorem is also related to an amusing incident.

It claims that two cops are accompanying a drunk. Both of these officers enter a cell, and despite the fact that the drunk is wobbling, he must also enter the cell. This is precisely how the theorem is used.

What is Squeeze Theorem?

The squeeze theorem (also known as the sandwich theorem) asserts that if a function f(x) is sandwiched between two functions g(x) and h(x), and the limits of both g(x) and h(x) at a given position are equal (to L), then the limit of f(x) at that point is likewise equal to L. This appears to be similar to what we already know from algebra. If a = c and b = c, then b must be equal to c as well. According to the squeeze theorem, this rule also applies to limits.

Squeeze Theorem Statement

“Let f(x), g(x), and h(x) are three functions that are defined over an interval I such that g(x) ≤ f(x) ≤ h(x) and suppose lim ₓ → ₐ g(x) = lim ₓ → ₐ h(x) = L, then lim ₓ → ₐ f(x) = L”.

Because f is between g and h, these are f’s lower and upper bounds, respectively.

‘a’ does not have to be contained within I.

Given the accompanying explanation, this theorem appears to be self-evident. Because f(x) is between g(x) and h(x), the graph of f(x) should be between the g(x) and h(x) curves. Furthermore, if both g(x) and h(x) tend to L as x a, f(x) cannot avoid having the same limit as L when x a. This is due to the fact that f(x) falls between the g(x) and h(x) curves (x).

Application of Squeeze Theorem

For example, the limit of a function of two variables at a location (a, b) is the finite value L, such that the function approaches the unique value L for any disc centred at (a, b) whose radius tends to zero (thus the disc approaches its centre):

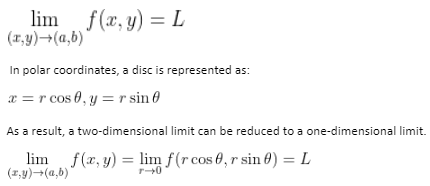
The Squeeze Theorem is commonly used to determine the limit in polar coordinates.

Importance of Squeeze Theorem

The Squeeze Theorem allows us to find the limit of complicated functions by squeezing them between two simpler functions

Squeeze Theorem’s derivation.

Knowing when it’s appropriate.

Using the Squeeze Theorem in a variety of situations. This theorem is especially relevant when working with functions that are the result of multiplying several sorts of expressions (such as the product of a polynomial and a trigonometric expression).

Important Notes of Squeeze Theorem

Remember the following trig inequalities when utilising the squeeze theorem (or sandwich theorem) to evaluate a limit.

Cos x < (sin x)/x < 1

-1 ≤ sin x ≤ 1, for any x in the domain of sin x

-1 ≤ cos x ≤ 1, for any x in the domain of cos x

Conclusion

In limit calculus, the squeeze theorem is a crucial topic. It is used to determine a function’s limit. Sandwich Theorem, Pinching Theorem, Squeeze Lemma, and Sandwich Rule are all names for the Squeeze Theorem.

The Sandwich theorem is used to discover the limit of a function when it gets difficult or intricate, or when other methods have failed to identify the limit.