An ordered pair is, as its name suggests, a pair of components that have distinct significance for the order in which they are positioned inside a structure. In the field of coordinate geometry, ordered pairs are most frequently utilised to represent a point on a coordinate plane. In addition to this, we may use them to represent different aspects of a relation.
Ordered pairs:
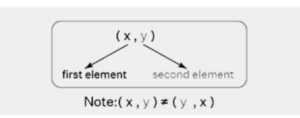
An ordered pair is a pair that is formed by two elements that are separated by a comma and written inside the parentheses. This type of pair is also known as an ordered pair. An example of an ordered pair would be the notation (x, y), where ‘x’ would be referred to as the first element of the ordered pair and ‘y’ would be referred to as the second element of the ordered pair. These constituents take on particular designations in accordance with the setting in which they are utilised, and they may take the form of either variables or constants. When looking at an ordered pair, it is important to pay attention to the order in which the pieces are presented. This indicates that it is possible for (x, y) to not always be equal to (y, x).
Examples of ordered pairs are the numbers (2,5) and the letters (a,b) as well as the numbers (a,-5) and so on.
Ordered pair in co – ordinate geometry:
In coordinate geometry, the position of a point on the coordinate plane with respect to the origin is represented by an ordered pair. This position is expressed as a distance from the origin. A coordinate plane is created when two lines that connect perpendicularly form a plane, with one of the lines being horizontal (the x-axis), and the other line being vertical (y-axis). The origin is located at the place where both axes connect with one another. The first element of an ordered pair is referred to as the x-coordinate, and the second element is referred to as the y-coordinate. This means that an ordered pair with the elements x and y represents every point on the coordinate plane. More distinctions can be made between the components of the ordered pair that are utilised in this application of geometry.
Graphing ordered pairs:
In the field of coordinate geometry, we are now aware of the distinction that exists between the x-coordinate and the y-coordinate of an ordered pair. Let’s have a look at the process of graphing ordered pairs now.
- Step 1: You will always begin at the origin, and you will travel horizontally by x units to the right if x is positive, and you will move horizontally by x units to the left if x is negative. Keep in place.
- Step 2: Beginning at the point where you stopped in Step 1, move vertically by y units, either upwards if y is positive or downwards if y is negative. This completes Step 2. Keep in place.
- Step 3: Exactly at the point where you stopped in Step 2, place a dot that represents the ordered pair. This dot will serve as the marker for the ordered pair (x, y)
In these steps, the values denoted by the notation |x| and |y| respectively indicate the absolute values of x and y.
Ordered pairs in different quadrants:
As may be seen in the illustration to the right, the x and y axes each subdivide the coordinate plane into one of four equal sections. The term “quadrant” refers to each of these four distinct sections. The table that follows illustrates how the signs of x and y in an ordered pair (x, y) of a point change depending on the quadrant at which the point is located.
Quadrants | Ordered pairs signs |
I | x>0, y>0 |
II | x<0, y>0 |
III | x<0, y<0 |
IV | x>0, y<0 |
Ordered pair in sets:
We have seen up to this point that ordered pairs are utilised in the process of locating a point in coordinate geometry. However, a separate application of these concepts can be found in the field of set theory. The cartesian product is a term used to describe the collection of all possible ordered pairings that can be transferred from one set A to another set B. For instance, if A = {1, 2, 3} and B = {a, b, c} then the cartesian product of A and B would be A x B = {(1, a), (1, b), (1, c), (2, a), (2, b), (3, c)} and it would be a set created by all ordered pairs (x, y) in which one member of the pair is from A and the other member is from B. A relation is a subset of the cartesian product that can be considered on its own. A relation could be written as {(1, a), (1, b), (3, c)} for instance.
Ordered pair of real numbers:
The first number a and the second number b together make up an ordered pair of real numbers that is denoted by the notation (a, b). For instance, the ordered pairs (1, 3), (3, 1), and (1, 1) are all distinct from one another. In keeping with established convention, we denote both the open interval (a, b) and the ordered pair with the same sign (a, b). On the other hand, the open interval and the ordered pair are two entirely distinct concepts. Whether or not the notation (a, b) refers to an open interval or an ordered pair will always be quite clear based on the surrounding circumstances.
Conclusion:
When indicating a position on a graph, it is common practise to use an ordered pair in which the “x” (horizontal) value comes first and the “y” (vertical) value comes second. A point can also be located using something called an ordered pair in the coordinate system. In mathematics, pairs are indicated by the symbol (,) and are typically assumed to be in order.
 Profile
Profile Settings
Settings Refer your friends
Refer your friends Sign out
Sign out






