Profile
Settings
Refer your friends
Sign out
As the angle between the two original vectors changes, the magnitude of the cross product of two vector quantities varies. The vector product of two vectors is another name for the cross product. The area of the parallelogram that they determine is the magnitude of a cross product. The cross product has an orthogonal (perpendicular) direction to the plane defined by the two vectors. Its magnitude is calculated by multiplying the magnitudes of the two angles by the sine of the angle between them. The corkscrew right-hand rule can be used to determine the vector product’s direction. The vector product of two vectors, either parallel or antiparallel, is zero.
What Does the Magnitude of the Cross Product of Two Vectors Represent?
The magnitude of the cross product represents the area of the parallelogram whose sides are defined by the two vectors. The magnitude is the area of the parallelogram spanned by a and b. (or length) of the vector a×b, written as |ab|.
As a result, the maximum value for the cross product occurs when the two vectors are perpendicular to. The magnitude of the cross product is zero when the two vectors are parallel to one another.
The Magnitude of Resultant of Cross Product
The product of the sine of the angle between the two vectors and their magnitudes determines the magnitude of the resultant vector.
A × B =|A| |B| sin θ.
As a result, the magnitude of A×B is very similar to that of the dot product. if A and B are parallel, the angle between them is zero, so sin=0, and |A×B|=0, similarly, if they are anti-parallel, sinθ=0, and |A×B|=0. If |A×B|=0 and |A| and |B| are not zero, then sinθ=0, indicating that A is parallel or anti-parallel to B.
We can join two vectors tail to tail to form a parallelogram, as shown in figure 1. The area of the parallelogram is |A||B|sinθ. The area of the parallelogram is |A||B|sinθ, and is the same as |AB|.., so the parallelogram’s height, h, is |A| sinθ and its base is |B|.
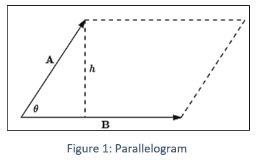
The direction can be described using a simple rule. Consider the following scenario:
Let A=⟨a,0,0⟩ and B= ⟨b,c,0⟩ Because A lies along the x-axis and B lies in the x-y plane when the vectors are placed with tails at the origin, we know the cross product will point up or down. The combined product is
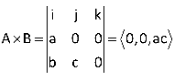
As expected, depending on the sign of ac, this is a vector pointing up or down. if c<0, the vector points down. When a<0 and c>0, however, the vector points down, whereas when a<0 and c<0, the vector points up.
Consider rotating vector A until it points in the same direction as B there are two ways to do this: use the rotation that goes through the smaller angle, or use the rotation that goes through the larger angle. When viewed from above, the rotation will be counter-clockwise if a>0 and c>0, or a<0 and c<0; in the other two cases, A must be rotated clockwise to reach B.
The rule is that clockwise means up and counter-clockwise means down. The same rule applies if A and B are any vectors in the x-y plane—A does not have to be parallel to the x-axis.
Then Place A and B side by side. View the plane in which A and B are located from two perspectives: from the side where A must rotate counter-clockwise to reach B, and from the side where the vector AB points toward you.
Because the two cross products point in opposite directions, one immediate consequence of these facts is that A×B≠B×A. Since, on the other hand,
|A×B|=|A||B|sinθ=|B||A|sinθ=|B×A|
We know that A×B=-(B×A) because the lengths of the two cross products are equal.
Magnitude of Cross Product Example
Example: Calculate the cross product of a=(3,-3,1) and b=(4,9,2)
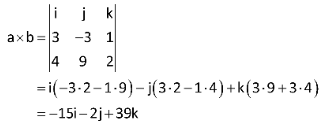
Conclusion
In this article we conclude that, the magnitude of the cross product vector is equal to the product of the magnitudes of the two vectors plus the sine of the angle between them. The area of a parallelogram with the vectors for sides equals the magnitude of the product; in particular, the magnitude of the product of two perpendicular vectors equals the product of their lengths. The size of a cross product used to calculate The area of the parallelogram that they determine is the magnitude of a cross product. The cross product has a direction that is orthogonal (perpendicular) to the plane defined by the two vectors.
